Coding a neural network layer

Introduction

In 1943, McCulloch and Pitts introduced artificial intelligence to the world. Their idea was to develop an algorithmic approach to mimic the functionality of the human brain. Due to the structure of the brain consisting of a net of neurons, they introduced the so-called artificial neurons as building blocks.

In it’s most simple form, the neuron consists of :

• dendrites, which receive the information from other neurons
• soma, which processes the information
• synapse, transmits the output of this neuron
• axon, point of connection to other neurons

Consequently, a mathematical definition of an artificial neuron is as follows.

Definition. An artificial neuron with weights \(w_1,\ldots,w_n \in \mathbf{R}\), bias \(b\in\mathbf{R}\) and an activation function \(\rho:\mathbf{R} \to \mathbf{R}\) is defined as the scalar-valued function \(f:\mathbf{R}^n \to \mathbf{R}\) given by:

\[\begin{align*} f(x_1,\ldots,x_n) = \rho \left(\sum_{i=1}^{n}w_i x_i + b\right) = \rho(\mathbf{w}^T \mathbf{x}+b) \tag{1} \end{align*}\]

where \(\mathbf{w} = (w_1,\ldots,w_n)\) and \(\mathbf{x}=(x_1,\ldots,x_n)\).

A single neuron by itself is useless, but when combined with hundreds or thousands(or many more) of other neurons, the interconnectivity can approximate any complex function and frequently outperforms any other machine learning methods.

%load_ext itikz

%%itikz --temp-dir --tex-packages=tikz --tikz-libraries=arrows --implicit-standalone
\begin{tikzpicture}
\foreach \i in {1,2}
{
    \node[circle, 
        minimum size = 15mm,
        fill=red!30
        ] (Input-\i) at (0,-\i * 2) {\large $x_\i$};
}
\foreach \i in {1,2,...,5}
{
    \node[circle, 
        minimum size = 15mm,
        fill=blue!50,
        yshift=30 mm
        ] (Hidden1-\i) at (3.0,-\i * 2) {\large $h_\i^{(1)}$};
        
}
\foreach \i in {1,2,...,5}
{
    \node[circle, 
        minimum size = 15mm,
        fill=blue!50,
        yshift=30 mm
        ] (Hidden2-\i) at (6.0,-\i * 2) {\large $h_\i^{(2)}$};
}
\foreach \i in {1,2}
{
    \node[circle, 
        minimum size = 15mm,
        fill=green!30] (Output-\i) at (9.0,-\i * 2) {\large $\hat{y}_\i$};
}

% Connect neurons In-Hidden1
\foreach \i in {1,...,2}
{
    \foreach \j in {1,...,5}
    {
        \draw[->, shorten >=1pt] (Input-\i) -- (Hidden1-\j);   
    }
}
\foreach \i in {1,...,5}
{
    \foreach \j in {1,...,5}
    {
        \draw[->, shorten >=1pt] (Hidden1-\i) -- (Hidden2-\j);   
    }
}
\foreach \i in {1,...,5}
{
    \foreach \j in {1,2}
    {
        \draw[->, shorten >=1pt] (Hidden2-\i) -- (Output-\j);   
    }
}
\end{tikzpicture}

Dense layers, the most common layers, consist of interconnected neurons. In a dense layer, each neuron of a given layer is connected to every neuron of the next layer, which means its output value becomes an input for the next neurons. Each connection between neurons has a weight associated with it, which is a trainable factor of how much of this input to use. Once all of the \(\text{inputs} \cdot \text{ weights}\) flow into our neuron, they are summed and a bias, another trainable parameter is added.

Say, we have an input \(x_1\) and weight \(w_1\), then the output \(y_1 = w_1 x_1\) is a straight-line with slope \(w_1\).

%%itikz --temp-dir --tex-packages=tikz,pgfplots --tikz-libraries=arrows --implicit-standalone
\begin{tikzpicture}[scale=1.5]
\begin{axis}
\addplot[color=blue]{x};
\addlegendentry{\(f(x)=x\)}
\addplot[color=red]{2*x};
\addlegendentry{\(f(x)=2x\)}
\end{axis}
\end{tikzpicture}

The bias offsets the overall function.

%%itikz --temp-dir --tex-packages=tikz,pgfplots --tikz-libraries=arrows --implicit-standalone
\begin{tikzpicture}[scale=1.5]
\begin{axis}
\addplot[color=black]{x+1};
\addlegendentry{\(f(x)=x+1\)}
\addplot[color=gray]{x-1};
\addlegendentry{\(f(x)=x-1\)}
\end{axis}
\end{tikzpicture}

Activation functions

Let us now look at some examples of activation functions.

The heaviside function is defined as:

\[\begin{align*} \rho(x) &= \begin{cases} 1, & x > 0 \\ 0, & x \leq 0 \end{cases} \end{align*}\]

The sigmoid function is defined as:

\[\begin{align*} \rho(x) &= \frac{1}{1+e^{-x}} \end{align*}\]

%%itikz --temp-dir --tex-packages=tikz,pgfplots --tikz-libraries=arrows --implicit-standalone
\begin{tikzpicture}[scale=1.5]
\begin{axis}
\addplot[color=black]{1/(1+exp(-x))};
\end{axis}
\end{tikzpicture}

The Rectifiable Linear Unit (ReLU) function is defined as:

\[\begin{align*} \rho(x) &= \max(0,x) \end{align*}\]

%%itikz --temp-dir --tex-packages=tikz,pgfplots --tikz-libraries=arrows --implicit-standalone
\begin{tikzpicture}[scale=1.5]
\begin{axis}
\addplot[color=black]{max(0,x)};
\end{axis}
\end{tikzpicture}

Coding a layer with 3-neurons

Let’s code a simple layer with \(n=3\) neurons.

inputs = [1, 2, 3, 2.5]
weights = [[0.2, 0.8, -0.5, 1.0], [0.5, -0.91, 0.26, -0.5], [-0.26, -0.27, 0.17, 0.87]]

biases = [2, 3, 0.5]

# Output of the current layer
layer_outputs = []

# For each neuron
for neuron_weights, neuron_bias in zip(weights, biases):
    # zeroed output of the neuron
    neuron_output = 0.0
    # for each input and weight to the neuron
    for input, weight in zip(inputs, neuron_weights):
        # multiply this input with the associated weight
        # and add to the neuron's output variable
        neuron_output += input * weight
    # Add bias
    neuron_output += neuron_bias
    # Put the neuron's result to the layer's output list
    layer_outputs.append(neuron_output)

print(layer_outputs)

[4.8, 1.21, 2.385]

We can achieve the same results as in our pure Python implementation of multiplying each component in our input vector \(\mathbf{x}\) and weights vector \(\mathbf{w}\) element-wise, by taking an inner product \(\mathbf{w} \cdot \mathbf{x}\).

import numpy as np

inputs = [1, 2, 3, 2.5]
weights = [
    [0.2, 0.8, -0.5, 1.0], 
    [0.5, -0.91, 0.26, -0.5], 
    [-0.26, -0.27, 0.17, 0.87]
]

biases = [2, 3, 0.5]

# Output of the current layer
layer_outputs = np.dot(weights, inputs) + biases

print(layer_outputs)

[4.8   1.21  2.385]

To train, neural networks tend to receive data in batches. So far, the example input data has only one sample (or observation) of various features called a feature set instance:

sample = [1, 2, 3, 2.5]

Often, neural networks expect to take in many samples at a time. One reason is its faster to train in batches in parallel processing. Also, if you fit on one sample at a time, you’re highly likely to keep fitting to that individual sample, rather than slowly producing general tweaks to the weights and biases that fit the entire dataset. Fitting or training in batches gives you a higher chance of making more meaningful changes to weights and biases.

A layer of neurons and a batch of data

Currently, the weights matrix looks as follows:

\[\begin{align*} W = \begin{bmatrix} 0.2 & 0.8 & -0.5 & 1.0 \\ 0.5 & -0.91 & 0.26 & -0.5 \\ -0.26 & -0.27 & 0.17 & 0.87 \end{bmatrix} \end{align*}\]

And say, that we have a batch of inputs:

\[\begin{align*} X = \begin{bmatrix} 1.0 & 2.0 & 3.0 & 3.5 \\ 2.0 & 5.0 & -1.0 & 2.0\\ -1.5 & 2.7 & 3.3 & -0.8 \end{bmatrix} \end{align*}\]

We need to take the inner products \((1.0, 2.0, 3.0, 3.5) \cdot (0.2, 0.8, -0.5, 1.0)\), \((2.0, 5.0, -1.0, 2.0) \cdot (0.2, 0.8, -0.5, 1.0)\) and \((-1.5, 2.7, 3.3, -0.8) \cdot (0.2, 0.8, -0.5, 1.0)\) for the first neuron.

We need to take the inner products \((1.0, 2.0, 3.0, 3.5) \cdot (0.5, -0.91, 0.26, -0.5)\), \((2.0, 5.0, -1.0, 2.0) \cdot (0.5, -0.91, 0.26, -0.5)\) and \((-1.5, 2.7, 3.3, -0.8) \cdot (0.5, -0.91, 0.26, -0.5)\) for the second neuron.

And so forth.

Consider the matrix product \(XW^T\):

\[\begin{align*} XW^T &= \begin{bmatrix} 1.0 & 2.0 & 3.0 & 2.5 \\ 2.0 & 5.0 & -1.0 & 2.0\\ -1.5 & 2.7 & 3.3 & -0.8 \end{bmatrix} \begin{bmatrix} 0.2 & 0.5 & -0.26 \\ 0.8 & -0.91 & -0.27 \\ -0.5 & 0.26 & 0.17 \\ 1.0 & -0.5 & 0.87 \end{bmatrix}\\ &= \begin{bmatrix} 2.8 & -1.79 & 1.885 \\ 6.9 & -4.81 & -0.3 \\ -0.59 & -1.949 & -0.474 \end{bmatrix} \end{align*}\]

import numpy as np

X = [
    [1.0, 2.0, 3.0, 2.5],
    [2.0, 5.0, -1.0, 2.0],
    [-1.5, 2.7, 3.3, -0.8]
]

W = [
    [0.2, 0.8, -0.5, 1.0],
    [0.5, -0.91, 0.26, -0.5],
    [-0.26, -0.27, 0.17, 0.87]
]

np.dot(X,np.array(W).T)

array([[ 2.8  , -1.79 ,  1.885],
       [ 6.9  , -4.81 , -0.3  ],
       [-0.59 , -1.949, -0.474]])

So, we can process a batch of inputs as:

layer_outputs = np.dot(X,np.array(W).T) + biases
print(layer_outputs)

[[ 4.8    1.21   2.385]
 [ 8.9   -1.81   0.2  ]
 [ 1.41   1.051  0.026]]

The second argument for np.dot() is going to be our transposed weights. Before, we were computing the neuron output using a single sample of data, but now we’ve taken a step forward where we model the layer behavior on a batch of data.

Adding Layers

The neural network we have built is becoming more respectable, but at the moment, we have only one layer. Neural networks become deep when they have \(2\) or more hidden layers. At the moment, we have just one layer, which is effectively an output layer. Why we want two or more hidden layers will become apparent later on. Currently, we have no hidden layers. A hidden layer isn’t an input or output layer; as the scientist, you see the data as they are handed to the input layer and the resulting data from the output layer. Layers between these endpoints have values that we don’t necessarily deal with, and hence the name “hidden”. Don’t let this name convince you that you can’t access these values, though. You will often use them to diagnose issues or improve your neural network. To explore this concept, let’s add another layer to this neural network, and for now, let’s assume that these two layers that we’re going to have will be hidden layers, and we just coded our output layer yet.

Before we add another layer, let’s think about what’s coming. In the case of the first layer, we can see that we have an input with \(4\) features.

%%itikz --temp-dir --tex-packages=tikz --tikz-libraries=arrows --implicit-standalone
\begin{tikzpicture}
\foreach \i in {1,2,...,4}
{
    \node[circle, 
        minimum size = 15mm,
        fill=red!30
        ] (Input-\i) at (0,-\i * 2) {\large $x_\i$};
}
\foreach \i in {1,2,...,3}
{
    \node[circle, 
        minimum size = 15mm,
        fill=blue!50,
        yshift=-10 mm
        ] (Hidden1-\i) at (3.0,-\i * 2) {\large $h_\i^{(1)}$};
        
}

% Connect neurons In-Hidden1
\foreach \i in {1,...,4}
{
    \foreach \j in {1,...,3}
    {
        \draw[->, shorten >=1pt] (Input-\i) -- (Hidden1-\j);   
    }
}
\end{tikzpicture}

Samples(feature set data) get fed through the input, which does not change it in any way, to our first hidden layer, which we can see has \(3\) sets of weights with \(4\) values each.

Each of those \(3\) unique weight sets is associated with its distinct neuron. Thus, since we have \(3\) weight sets, we have \(3\) neurons in the first hidden layer. Each neuron has a unique set of weights, of which we have \(4\) (as there are \(4\) inputs to this layer), which is why our initial weights have a shape of \((3,4)\).

Now we wish to add another layer. To do that, we must make sure that the expected input to that layer matches the previous layer’s output. We have set the number of neurons in a layer by setting how many weights and biases we have. The previous layer’s influence on weight sets for the current layer is that each weight set needs to have a separate weight per input. This means a distinct weight per neuron from the previous layer (or feature if we’re talking the input). The previous layer has \(3\) weight sets and \(3\) biases, so we know it has \(3\) neurons. This then means, for the next layer, we can have as many weight sets as we want (because this is how many neurons this new layer will have), but each of those weight sets must have \(3\) discrete weights.

To create this new layer, we are going to copy and paste our weights and biases to weights2 and biases2, and change their values to new made up sets. Here’s an example:

inputs = [
    [1, 2, 3, 2.5],
    [2.0, 5.0, -1.0, 2],
    [-1.5, 2.7, 3.3, -0.8]
]

weights = [
    [0.2, 0.8, -0.5, 1],
    [0.5, -0.91, 0.26, -0.5],
    [-0.26, -0.27, 0.17, 0.87]
]

biases = [2, 3, 0.5]

weights2 = [
    [0.1, -0.14, 0.5],
    [-0.5, 0.12, -0.33],
    [-0.44, 0.73, -0.13]
]

biases2 = [-1, 2, -0.5]

Next, we will now call the outputs layer1_outputs.

layer1_outputs = np.dot(inputs, np.array(weights).T) + biases

As previously stated, inputs to the layers are either inputs from the actual dataset you’re training with, or outputs from a previous layer. That’s why we defined \(2\) versions of weights and biases, but only one of inputs.

layer2_outputs = np.dot(layer1_outputs, np.array(weights2).T) + biases2

At this point, our neural network could be visually represented as:

%%itikz --temp-dir --tex-packages=tikz --tikz-libraries=arrows --implicit-standalone
\begin{tikzpicture}
\foreach \i in {1,2,...,4}
{
    \node[circle, 
        minimum size = 15mm,
        fill=red!30
        ] (Input-\i) at (0,-\i * 2) {\large $x_\i$};
}
\foreach \i in {1,2,...,3}
{
    \node[circle, 
        minimum size = 15mm,
        fill=blue!50,
        yshift=-10 mm
        ] (Hidden1-\i) at (3.0,-\i * 2) {\large $h_\i^{(1)}$};
        
}
\foreach \i in {1,2,...,3}
{
    \node[circle, 
        minimum size = 15mm,
        fill=blue!50,
        yshift=-10 mm
        ] (Hidden2-\i) at (6.0,-\i * 2) {\large $h_\i^{(2)}$};
        
}

% Connect neurons In-Hidden1
\foreach \i in {1,...,4}
{
    \foreach \j in {1,...,3}
    {
        \draw[->, shorten >=1pt] (Input-\i) -- (Hidden1-\j);   
    }
}
% Connect neurons Hidden1-Hidden2
\foreach \i in {1,...,3}
{
    \foreach \j in {1,...,3}
    {
        \draw[->, shorten >=1pt] (Hidden1-\i) -- (Hidden2-\j);   
    }
}
\end{tikzpicture}

Training Data

Next, rather than hand-typing in random data, we’ll use a function that can create non-linear data. What do we mean by non-linear? Linear data can be fit or represented by a straight line. Non-linear data cannot be represented well by a straight line.

We shall use the python package nnfs to create data. You can install it with

pip install nnfs

You typically don’t generate training data from a package like nnfs for your neural networks. Generating a dataset this way is purely for convenience at this stage. I shall also use this package to ensure repeatability.

import numpy as np
import nnfs

nnfs.init()

The nnfs.init() does three things: it sets the random seed to \(0\) by default, creates a float32 dtype default and overrides the original dot product from numpy. All of these are meant to ensure repeatable results for following along.

from nnfs.datasets import spiral_data
import matplotlib.pyplot as plt

X, y = spiral_data(samples=100, classes=3)

plt.scatter(X[:,0], X[:,1])
plt.show()

The spiral_data function allows us to create a dataset with as many classes as we want. The function has parameters to choose the number of classes and the number of points/observations per class in the resulting non-linear dataset.

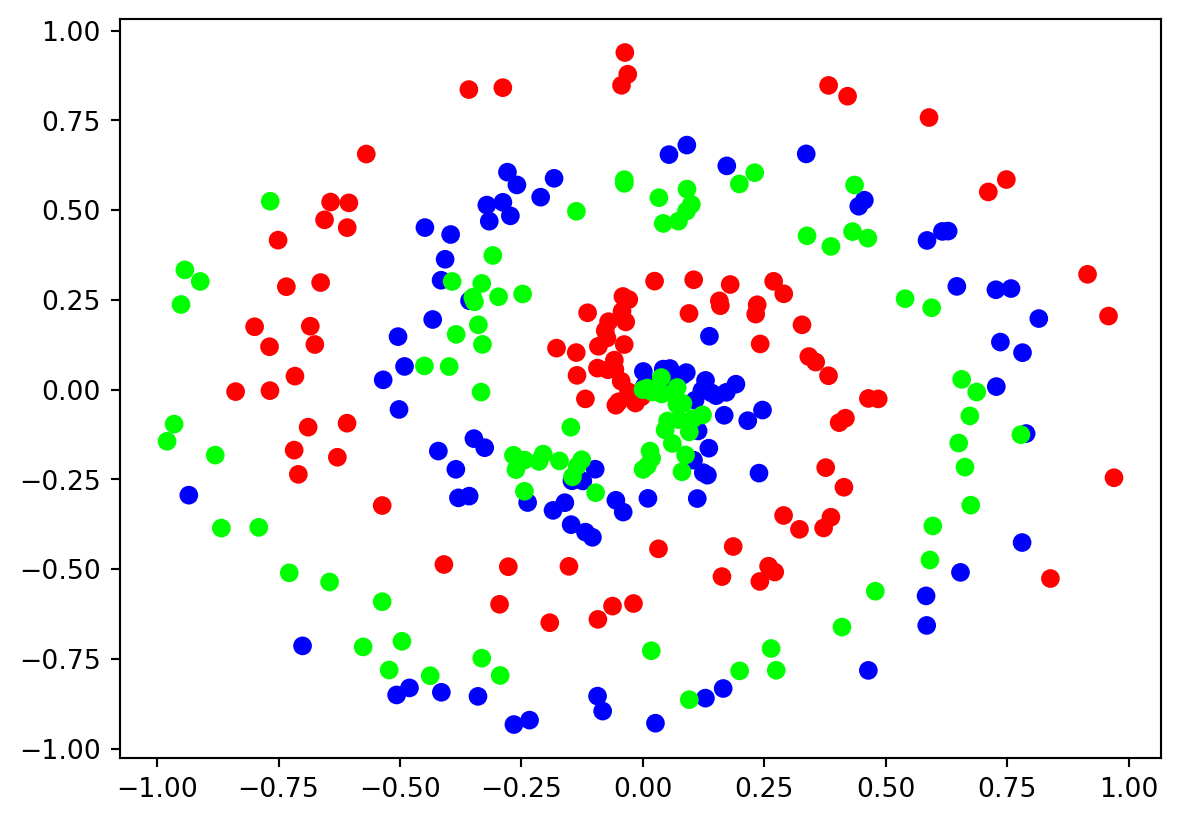
If you trace from the center, you can determine all \(3\) classes separately, but this is a very challenging problem for a machine learning classifier to solve. Adding color to the chart makes this more clear:

plt.scatter(X[:,0],X[:,1],c=y,cmap='brg')
plt.show()

Keep in mind that the neural network will not be aware of the color differences as the data have no class encodings. This is only made as an instruction for you. In the data above, each dot is an observation, that is, it’s coordinates are the samples that form the dataset. The classification for the dot has to do with which spiral it is a part of, depicted by red, blue or green color.

Dense Layer Class

Now that we no longer need to hand-type our data, we should create something similar for our various types of neural network layers. So far, we’ve only used what’s called a dense or fully-connected layer. These layers are commonly referred to as dense layers in papers, literature and code, but you will see them called fully-connected or fc for short in the code I write. Our dense layer class begins with two methods:

class DenseLayer:
    def __init__(self, n_inputs, n_neurons):
        # Initialize weights and biases
        pass # using pass statement as a placeholder

    # Forward pass
    def forward(self, inputs):
        # Calculate output values from inputs, weights and biases
        pass # using pass statement as a placeholder

Weights are often initialized randomly for a model, but not always. If you wish to load a pre-trained model, you will initialize the parameters to whatever that pretrained model finished with. It’s also possible that, even for a new model, you have some other initialization rules besides random. From now, we’ll stick with random initialization. Next, we have the forward method. When we pass data through a model from beginning to end, this is called a forward pass. Just like everything else, this is not the only way to do things. You can have the data loop back around and do other interesting things. We’ll keep it usual and perform a regular forward pass.

To continue the LayerDense class code, let’s add the random initialization of weights and biases:

#Layer initialization
def __init__(self,n_inputs, n_neurons):
    self.weights = 0.01 * np.random.randn(n_inputs,n_neurons)
    self.biases = np.zeros((1,n_neurons))

Here, we are setting the weights to be random and the biases to be \(0\). Note that, we are initializing weights to be a matrix of dimensions \(n_{inputs} \times n_{neurons}\), rather than \(n_{neurons} \times n_{inputs}\). We’re doing this ahead instead of transposing everytime we perform a forward pass, as explained in the previous chapter.

We initialize the biases to zero, because with many samples containing values of \(0\), it will ensure that a neuron fires initially. The most common initialization for biases is zero. This will vary depending on our use-case and is just one of the many things we can tweak when trying to improve results. One situation where we might want to try something else is with what’s called dead neurons.

Imagine our step function again:

\[\begin{align*} y = \begin{cases} 1, & x > 0\\ 0, & x \leq 0 \end{cases} \end{align*}\]

It’s possible for \(\text{weights} \cdot \text{inputs} + \text{biases}\) not to meet the threshold of the step function, which means the neuron will output a zero. On its own, this is not a big issue, but it becomes a problem if this happens to this neuron for every one of the input samples (it’ll become clear why once we learn about backpropogation). So, then this neuron’s \(0\) output is the input to another neuron. Any weight multiplied by zero will be zero. With an increasing number of neurons outputting \(0\), more inputs to the next neurons will be zeros, rendering the network essentially non-trainable or dead.

On to our forward method now.

class DenseLayer:
    def __init__(self, n_inputs, n_neurons):
        self.weights = 0.01 * np.random.randn(n_inputs,n_neurons)
        self.biases = np.zeros((1,n_neurons))

    def forward(self,inputs):
        self.output = np.dot(inputs,self.weights) + self.biases

We are now ready to make use of this new class instead of hardcoded calculations, so let’s generate some data using the discussed dataset creation method and use our new layer to perform a forward pass:

# Create dataset
X, y = spiral_data(samples=100, classes=3)

# Create a dense layer with 2 input features and 3 output values
dense1 = DenseLayer(2, 3)

# Perform a forward pass of our training data through this layer
dense1.forward(X)

# Let's see the output of the first few samples
print(dense1.output[:5])

[[ 0.00000000e+00  0.00000000e+00  0.00000000e+00]
 [-1.11171044e-04 -5.11007493e-05 -1.12099799e-04]
 [ 2.99257295e-06 -2.69126613e-04 -1.45165104e-04]
 [ 8.95101766e-05 -4.30442247e-04 -1.68079801e-04]
 [-3.49893759e-04 -3.07208364e-04 -4.33002861e-04]]

Activation Functions

We use activation functions because if the activation function itself is non-linear, it allows for neural networks with two or more layers to map non-linear functions. We’ll see how this works. In general, your neural network will have \(2\) types of activation functions. The first will be the activation function used in hidden layers, and the second will be used in the output layer. Usually, the activation function used for hidden neurons will be all the same for all of them, but it doesn’t have to.

Why use activation functions?

Let’s discuss why we use activation functions in the first place? In most cases, for a neural network to fit a non-linear function, we need it to contain two or more hidden layers and we need those hidden layers to use a non-linear activation function.

While there are certainly problems in life that are linear in nature, for example, trying to figure out the cost of some number of shirts, and we know the cost of an individual shirt, then the equation to calculate the price of any number of those products is a linear equation; other problems in life are not so simple.

Many interesting and hard problems are non-linear. The main attraction of neural networks has to do with their ability to solve non-linear problems. If we allow only linear activation functions in a neural network, the output will just be a linear transformation of the input, which is not enough to form a universal function approximator.

For simplicity, suppose a neural network has \(2\) hidden layers with \(1\) neuron each.

%%itikz --temp-dir --tex-packages=tikz --tikz-libraries=arrows --implicit-standalone
\begin{tikzpicture}[scale=1.5]
    \node[circle, 
        minimum size = 15mm,
        fill=red!30
        ] (Input) at (0,0) {\large $x_1$};

    \node[circle, 
        minimum size = 15mm,
        fill=blue!50
        ] (Hidden1) at (3.0,0) {\large $h_1^{(1)}$};
        

    \node[circle, 
        minimum size = 15mm,
        fill=blue!50
        ] (Hidden2) at (6.0,0) {\large $h_1^{(2)}$};

    \node[circle, 
        minimum size = 15mm,
        fill=red!30
        ] (Output) at (9.0,0) {\large $\hat{y}_1$};        
        

    \draw[->, shorten >=1pt] (Input) -- (Hidden1) node [midway,above] {\large $w_1$};
    \draw[->, shorten >=1pt] (Hidden1) -- (Hidden2) node [midway,above]  {\large $w_2$};
    \draw[->, shorten >=1pt] (Hidden2) -- (Output);
    \draw[->, shorten >=1pt] (3.0, -2.0) node [below] {\large $b_1$} -- (Hidden1);
    \draw[->, shorten >=1pt] (6.0, -2.0) node [below] {\large $b_2$} -- (Hidden2);
\end{tikzpicture}

\[\begin{align*} \hat{y}_1 &= h_1^{(2)} \\ &= w_2 h_1^{(1)} + b_2 \\ &= w_2 (w_1 x_1 + b_1) + b_2 \\ &= w_2 w_1 x_1 + (w_2 b_1 + b_2) \end{align*}\]

So, \(\hat{y}_1\) is a linear function of the inputs, no matter, what values we choose for weights and biases.

The composition of linear functions is linear. No matter what we do, however many layers we have, or neurons we have in each layer, this network can only model linear functions.

ReLU Activation in a pair of Neurons

It is less obvious how, with a barely non-linear activation function, like the rectified linear activation function, we can suddenly model non-linear relationships and functions. Let’s start with a single neuron. We’ll begin with both a weight of zero and a bias of zero:

%%itikz --temp-dir --tex-packages=tikz --tikz-libraries=arrows --implicit-standalone
\begin{tikzpicture}[scale=1.5]
    \node[circle, 
        minimum size = 15mm,
        draw=blue
        ] (Input) at (0,0) {};
    
    \node[] (w) at (-3,0) {};
    \node[] (b) at (0,-2) {};

    \draw[->, shorten >=1pt] (w) -- (Input) node [midway,above] {\large $0.00$};
    \draw[->, shorten >=1pt] (b) node [below] {\large $0.00$} -- (Input);
\end{tikzpicture}

In this case, no matter what input we pass, the output of this neuron will always be \(0\), because the weight is \(0\) and the bias is \(0\).

%%itikz --temp-dir --tex-packages=tikz,pgfplots --tikz-libraries=arrows --implicit-standalone
\begin{tikzpicture}[scale=1.5]
\begin{axis}[grid]
\addplot[color=blue,thick]{0};
\end{axis}
\end{tikzpicture}

Let’s set the weight to be \(1.00\).

%%itikz --temp-dir --tex-packages=tikz --tikz-libraries=arrows --implicit-standalone
\begin{tikzpicture}[scale=1.5]
    \node[circle, 
        minimum size = 15mm,
        draw=blue
        ] (Input) at (0,0) {};
    
    \node[] (w) at (-3,0) {};
    \node[] (b) at (0,-2) {};

    \draw[->, shorten >=1pt] (w) -- (Input) node [midway,above] {\large $1.00$};
    \draw[->, shorten >=1pt] (b) node [below] {\large $0.00$} -- (Input);
\end{tikzpicture}

Now, it just looks like the basic rectified linear function. No surprises yet!

%%itikz --temp-dir --tex-packages=tikz,pgfplots --tikz-libraries=arrows --implicit-standalone
\begin{tikzpicture}[scale=1.5]
\begin{axis}[grid,ymin=-2.0,ymax=2.0,xmin=-2.0,xmax=2.0]
\addplot[color=blue,thick]{max(x,0)};
\end{axis}
\end{tikzpicture}

Now, let’s set the bias to \(0.50\):

%%itikz --temp-dir --tex-packages=tikz --tikz-libraries=arrows --implicit-standalone
\begin{tikzpicture}[scale=1.5]
    \node[circle, 
        minimum size = 15mm,
        draw=blue
        ] (Input) at (0,0) {};
    
    \node[] (w) at (-3,0) {};
    \node[] (b) at (0,-2) {};

    \draw[->, shorten >=1pt] (w) -- (Input) node [midway,above] {\large $1.00$};
    \draw[->, shorten >=1pt] (b) node [below] {\large $0.50$} -- (Input);
\end{tikzpicture}

We can see that in this case, with a single neuron, the bias offsets the overall function’s activation point horizontally.

%%itikz --temp-dir --tex-packages=tikz,pgfplots --tikz-libraries=arrows --implicit-standalone
\begin{tikzpicture}[scale=1.5]
\begin{axis}[grid,ymin=-2.0,ymax=2.0,xmin=-2.0,xmax=2.0]
\addplot[color=blue,thick,samples=100]{max(x+0.50,0)};
\end{axis}
\end{tikzpicture}

By increasing bias, we’re making this neuron activate earlier. What happens when we negate the weight to \(-1.0\)?

%%itikz --temp-dir --tex-packages=tikz --tikz-libraries=arrows --implicit-standalone
\begin{tikzpicture}[scale=1.5]
    \node[circle, 
        minimum size = 15mm,
        draw=blue
        ] (Input) at (0,0) {};
    
    \node[] (w) at (-3,0) {};
    \node[] (b) at (0,-2) {};

    \draw[->, shorten >=1pt] (w) -- (Input) node [midway,above] {\large $-1.00$};
    \draw[->, shorten >=1pt] (b) node [below] {\large $0.50$} -- (Input);
\end{tikzpicture}

With a negative weight and this single neuron, the function has become a question of when this neuron deactivates.

%%itikz --temp-dir --tex-packages=tikz,pgfplots --tikz-libraries=arrows --implicit-standalone
\begin{tikzpicture}[scale=1.5]
\begin{axis}[grid,ymin=-2.0,ymax=2.0,xmin=-2.0,xmax=2.0]
\addplot[color=blue,thick,samples=100]{max(-x+0.50,0)};
\end{axis}
\end{tikzpicture}

What happens if modify the weight to \(-2.00\)?

%%itikz --temp-dir --tex-packages=tikz --tikz-libraries=arrows --implicit-standalone
\begin{tikzpicture}[scale=1.5]
    \node[circle, 
        minimum size = 15mm,
        draw=blue
        ] (Input) at (0,0) {};
    
    \node[] (w) at (-3,0) {};
    \node[] (b) at (0,-2) {};

    \draw[->, shorten >=1pt] (w) -- (Input) node [midway,above] {\large $-2.00$};
    \draw[->, shorten >=1pt] (b) node [below] {\large $0.50$} -- (Input);
\end{tikzpicture}

The neuron now deactivates at \(0.25\).

%%itikz --temp-dir --tex-packages=tikz,pgfplots --tikz-libraries=arrows --implicit-standalone
\begin{tikzpicture}[scale=1.5]
\begin{axis}[grid,ymin=-2.0,ymax=2.0,xmin=-2.0,xmax=2.0]
\addplot[color=blue,thick,samples=100]{max(-2*x+0.50,0)};
\end{axis}
\end{tikzpicture}

Upto this point, we’ve seen how we can use the bias to offset the function horizontally, and the weight to influence the slope of the activation. Moreover, we’re also able to control whether the function is one for determining where the neuron activates or deactivates. What happens when we have, rather than just one neuron, a pair of neurons? For example, let’s pretend that we have two hidden layers of \(1\) neuron each. Thinking back to the \(y=x\) activation function, we unsurprisingly discovered that a linear activation function produced linear results no matter what chain of neurons we made. Let’s see what happens with the rectified linear function for the activation.

We’ll begin with the last values for the first neuron and a weight of \(1.00\) and a bias of \(0.00\) for the second neuron.

%%itikz --temp-dir --tex-packages=tikz --tikz-libraries=arrows --implicit-standalone
\begin{tikzpicture}[scale=1.5]
    \node[circle, 
        minimum size = 15mm,
        draw=blue
        ] (Input) at (0,0) {};

    \node[circle, 
        minimum size = 15mm,
        draw=blue
        ] (Hidden1) at (3,0) {};
    
    \node[] (w1) at (-3,0) {};
    \node[] (b1) at (0,-2) {};
    \node[] (b2) at (3,-2) {};

    \draw[->, shorten >=1pt] (w1) -- (Input) node [midway,above] {\large $-1.00$};
    \draw[->, shorten >=1pt] (b1) node [below] {\large $0.50$} -- (Input);
    \draw[->, shorten >=1pt] (Input) -- (Hidden1) node [midway,above] {\large $1.00$};
    \draw[->, shorten >=1pt] (b2) node [below] {\large $0.00$} -- (Hidden1);
\end{tikzpicture}

As we can see so far, there’s no change. This is because the second neuron’s bias is doing no offsetting, and the second neuron’s weight is just multiplying the output by \(1\), so there’s no change. Let’s try to adjust the second neuron’s bias now:

%%itikz --temp-dir --tex-packages=tikz,pgfplots --tikz-libraries=arrows --implicit-standalone
\begin{tikzpicture}[scale=1.5]
\begin{axis}[grid,ymin=-1,ymax=6,ytick={-1,0,...,6}]
\addplot[color=blue,thick,samples=100]{max(max(-x+0.50,0),0)};
\end{axis}
\end{tikzpicture}

Let’s try to adjust the second neuron’s bias now:

%%itikz --temp-dir --tex-packages=tikz --tikz-libraries=arrows --implicit-standalone
\begin{tikzpicture}[scale=1.5]
    \node[circle, 
        minimum size = 15mm,
        draw=blue
        ] (Input) at (0,0) {};

    \node[circle, 
        minimum size = 15mm,
        draw=blue
        ] (Hidden1) at (3,0) {};
    
    \node[] (w1) at (-3,0) {};
    \node[] (b1) at (0,-2) {};
    \node[] (b2) at (3,-2) {};

    \draw[->, shorten >=1pt] (w1) -- (Input) node [midway,above] {\large $-1.00$};
    \draw[->, shorten >=1pt] (b1) node [below] {\large $0.50$} -- (Input);
    \draw[->, shorten >=1pt] (Input) -- (Hidden1) node [midway,above] {\large $1.00$};
    \draw[->, shorten >=1pt] (b2) node [below] {\large $1.00$} -- (Hidden1);
\end{tikzpicture}

Now, we see some fairly interesting behavior. The bias of the second neuron indeed shifted the overall function but, rather than shifting it horizontally, it shifted vertically.

%%itikz --temp-dir --tex-packages=tikz,pgfplots --tikz-libraries=arrows --implicit-standalone
\begin{tikzpicture}[scale=1.5]
\begin{axis}[grid,ymin=-1,ymax=6,ytick={-1,0,...,6}]
\addplot[color=blue,thick,samples=100]{max(max(-x+0.50,0)+1.00,0)};
\end{axis}
\end{tikzpicture}

What then might happen, if we make the \(2\)nd neuron’s weight \(-2\) rather than \(1\)?

%%itikz --temp-dir --tex-packages=tikz --tikz-libraries=arrows --implicit-standalone
\begin{tikzpicture}[scale=1.5]
    \node[circle, 
        minimum size = 15mm,
        draw=blue
        ] (Input) at (0,0) {};

    \node[circle, 
        minimum size = 15mm,
        draw=blue
        ] (Hidden1) at (3,0) {};
    
    \node[] (w1) at (-3,0) {};
    \node[] (b1) at (0,-2) {};
    \node[] (b2) at (3,-2) {};

    \draw[->, shorten >=1pt] (w1) -- (Input) node [midway,above] {\large $-1.00$};
    \draw[->, shorten >=1pt] (b1) node [below] {\large $0.50$} -- (Input);
    \draw[->, shorten >=1pt] (Input) -- (Hidden1) node [midway,above] {\large $-2.00$};
    \draw[->, shorten >=1pt] (b2) node [below] {\large $1.00$} -- (Hidden1);
\end{tikzpicture}

Something exciting has occurred! What we have here is a neuron that has both an activation and a deactivation point. Now, the output after these two neurons will be variable, so long as it is inside of some specific range. So, basically if both neurons are activated then we actually sort of see this influence on the value. Otherwise, if both neurons aren’t activated, then the output is just a static value.

%%itikz --temp-dir --tex-packages=tikz,pgfplots --tikz-libraries=arrows --implicit-standalone
\begin{tikzpicture}[scale=1.5]
\begin{axis}[grid,ymin=-1,ymax=2,ytick={-1,0,...,2},xmin=-2,xmax=2]
\addplot[color=blue,thick,samples=500]{max(-2.0*max(-x+0.50,0)+1.00,0)};
\end{axis}
\end{tikzpicture}

So, when we are below the activation of the first neuron, the output will be the bias of the second neuron \(1.00\).

%%itikz --temp-dir --tex-packages=tikz --tikz-libraries=arrows --implicit-standalone
\begin{tikzpicture}[scale=1.5]
    \node[circle, 
        minimum size = 15mm,
        draw=blue
        ] (Input) at (0,0) {};

    \node[circle, 
        minimum size = 15mm,
        draw=blue,
        fill=green
        ] (Hidden1) at (3,0) {};
    
    \node[] (w1) at (-3,0) {};
    \node[] (b1) at (0,-2) {};
    \node[] (b2) at (3,-2) {};

    \draw[->, shorten >=1pt] (w1) node [left] {\large $0.50$} -- (Input) node [midway,above] {\large $-1.00$};
    \draw[->, shorten >=1pt] (b1) node [below] {\large $0.50$} -- (Input);
    \draw[->, shorten >=1pt] (Input) -- (Hidden1) node [midway,above] {\large $-2.00$};
    \draw[->, shorten >=1pt] (b2) node [below] {\large $1.00$} -- (Hidden1);
    \draw[->, shorten >=1pt] (Hidden1) -- (6,0) node [right] {$1.00$};
\end{tikzpicture}

The second neuron is activated if it’s input is smaller than \(0.50\).

Consider what happens when the input to the first neuron is \(0.00, -0.10, \ldots\). The output of the first neuron is \(0.50, 0.60, \ldots\) which implies that the second neuron is deactivated, so the output of the second neuron is simply zero.

%%itikz --temp-dir --tex-packages=tikz --tikz-libraries=arrows --implicit-standalone
\begin{tikzpicture}[scale=1.5]
    \node[circle, 
        minimum size = 15mm,
        draw=blue,
        fill=green
        ] (Input) at (0,0) {};

    \node[circle, 
        minimum size = 15mm,
        draw=blue
        ] (Hidden1) at (3,0) {};
    
    \node[] (w1) at (-3,0) {};
    \node[] (b1) at (0,-2) {};
    \node[] (b2) at (3,-2) {};

    \draw[->, shorten >=1pt] (w1) node [left] {\large $0.50$} -- (Input) node [midway,above] {\large $-1.00$};
    \draw[->, shorten >=1pt] (b1) node [below] {\large $0.50$} -- (Input);
    \draw[->, shorten >=1pt] (Input) -- (Hidden1) node [midway,above] {\large $-2.00$};
    \draw[->, shorten >=1pt] (b2) node [below] {\large $1.00$} -- (Hidden1);
    \draw[->, shorten >=1pt] (Hidden1) -- (6,0) node [right] {$0.00$};
\end{tikzpicture}

ReLU Activation in hidden layers

Let’s now take this concept and use it to fit to a sine wave-like function using two hidden layers of \(8\) neurons each and we can hand-tune the values to fit the curve. We’ll do this by working with \(1\) pair of neurons at a time, which means \(1\) neuron from each layer individually. For simplicity, we are also going to assume that the layers are not densely connected, and each neuron from the first hidden layer connects to only one neuron from the second hidden layer. That’s usually not the case with the real models, but we want this simplification for the purpose of this demo. Additionally, this example model takes a single value as an input, the input to the sine function, and outputs a single value like the sine function. The output layer uses the linear activation function and the hidden layers will use the rectified linear activation function.

To start, we’ll set all weights to \(0\) and work with the first pair of neurons:

%%itikz --temp-dir --tex-packages=tikz --tikz-libraries=arrows --implicit-standalone
\begin{tikzpicture}

\node[circle, 
    minimum size = 15mm,
    fill=red!30
    ] (Input) at (0,0) {\large $x_1$};

\foreach \i in {1,2,...,8}
{
    \node[circle, 
        minimum size = 15mm,
        fill=blue!50,
        yshift=90 mm
        ] (Hidden1-\i) at (3.0,-\i * 2) {\large $h_\i^{(1)}$};
        
}
\foreach \i in {1,2,...,8}
{
    \node[circle, 
        minimum size = 15mm,
        fill=blue!50,
        yshift=90 mm
        ] (Hidden2-\i) at (6.0,-\i * 2) {\large $h_\i^{(2)}$};
        
}

\node[circle, 
    minimum size = 15mm,
    fill=red!30
    ] (Output) at (9,0) {\large $\hat{y}_1$};

% Connect neurons In-Hidden1
\foreach \j in {2,...,8}
{
    \draw[->, shorten >=1pt] (Input) -- (Hidden1-\j);   
}
% Connect neurons Hidden1-Hidden2
\foreach \i in {2,...,8}
{
    
        \draw[->, shorten >=1pt] (Hidden1-\i) -- (Hidden2-\i);   
    
}

\foreach \i in {2,...,8}
{
    
        \draw[->, shorten >=1pt] (Hidden2-\i) -- (Output);   
}
\draw[->, shorten >=1pt] (Input) -- node [midway] {$0.00$} (Hidden1-1);   
\draw[->, shorten >=1pt] (Hidden1-1) -- node [midway] {$0.00$} (Hidden2-1); 
\draw[->, shorten >=1pt] (Hidden2-1) -- node [midway] {$0.00$} (Output); 
\draw[->, shorten >=1pt] (6,6) node [below] {$0.00$} --  (Hidden2-1); 
\draw[->, shorten >=1pt] (3,6) node [below] {$0.00$} --  (Hidden1-1); 
\end{tikzpicture}

Next, we can set the weight for the hidden layer neurons and the output neuron to \(1.00\), and we can see how this impacts the output:

%%itikz --temp-dir --tex-packages=tikz --tikz-libraries=arrows --implicit-standalone
\begin{tikzpicture}

\node[circle, 
    minimum size = 15mm,
    fill=red!30
    ] (Input) at (0,0) {\large $x_1$};

\foreach \i in {1,2,...,8}
{
    \node[circle, 
        minimum size = 15mm,
        fill=blue!50,
        yshift=90 mm
        ] (Hidden1-\i) at (3.0,-\i * 2) {\large $h_\i^{(1)}$};
        
}
\foreach \i in {1,2,...,8}
{
    \node[circle, 
        minimum size = 15mm,
        fill=blue!50,
        yshift=90 mm
        ] (Hidden2-\i) at (6.0,-\i * 2) {\large $h_\i^{(2)}$};
        
}

\node[circle, 
    minimum size = 15mm,
    fill=red!30
    ] (Output) at (9,0) {\large $\hat{y}_1$};

% Connect neurons In-Hidden1
\foreach \j in {2,...,8}
{
    \draw[->, shorten >=1pt] (Input) -- (Hidden1-\j);   
}
% Connect neurons Hidden1-Hidden2
\foreach \i in {2,...,8}
{
    
        \draw[->, shorten >=1pt] (Hidden1-\i) -- (Hidden2-\i);   
    
}

\foreach \i in {2,...,8}
{
    
        \draw[->, shorten >=1pt] (Hidden2-\i) -- (Output);   
}
\draw[->, shorten >=1pt] (Input) -- node [midway] {$1.00$} (Hidden1-1);   
\draw[->, shorten >=1pt] (Hidden1-1) -- node [midway,above] {$1.00$} (Hidden2-1); 
\draw[->, shorten >=1pt] (Hidden2-1) -- node [midway] {$1.00$} (Output); 
\draw[->, shorten >=1pt] (6,6) node [below] {$0.00$} --  (Hidden2-1); 
\draw[->, shorten >=1pt] (3,6) node [below] {$0.00$} --  (Hidden1-1); 
\end{tikzpicture}

The output is:

%%itikz --temp-dir --tex-packages=tikz,pgfplots --tikz-libraries=arrows --implicit-standalone
\begin{tikzpicture}[scale=1.5]
\begin{axis}[grid,ymin=-2,ymax=2,ytick={-2,-1,...,2},xmin=0,xmax=1]
\addplot[color=blue,thick,samples=1000]{max(max(x,0),0)};
\addplot[color=green,samples=1000,domain=0:1]{sin(deg(2*3.14*x))};
\end{axis}
\end{tikzpicture}

We can increase the slope of the output by adjusting the weight of the first neuron of the first layer to \(6.00\).

%%itikz --temp-dir --tex-packages=tikz --tikz-libraries=arrows --implicit-standalone
\begin{tikzpicture}

\node[circle, 
    minimum size = 15mm,
    fill=red!30
    ] (Input) at (0,0) {\large $x_1$};

\foreach \i in {1,2,...,8}
{
    \node[circle, 
        minimum size = 15mm,
        fill=blue!50,
        yshift=90 mm
        ] (Hidden1-\i) at (3.0,-\i * 2) {\large $h_\i^{(1)}$};
        
}
\foreach \i in {1,2,...,8}
{
    \node[circle, 
        minimum size = 15mm,
        fill=blue!50,
        yshift=90 mm
        ] (Hidden2-\i) at (6.0,-\i * 2) {\large $h_\i^{(2)}$};
        
}

\node[circle, 
    minimum size = 15mm,
    fill=red!30
    ] (Output) at (9,0) {\large $\hat{y}_1$};

% Connect neurons In-Hidden1
\foreach \j in {2,...,8}
{
    \draw[->, shorten >=1pt] (Input) -- (Hidden1-\j);   
}
% Connect neurons Hidden1-Hidden2
\foreach \i in {2,...,8}
{
    
        \draw[->, shorten >=1pt] (Hidden1-\i) -- (Hidden2-\i);   
    
}

\foreach \i in {2,...,8}
{
    
        \draw[->, shorten >=1pt] (Hidden2-\i) -- (Output);   
}
\draw[->, shorten >=1pt] (Input) -- node [midway] {$6.00$} (Hidden1-1);   
\draw[->, shorten >=1pt] (Hidden1-1) -- node [midway,above] {$1.00$} (Hidden2-1); 
\draw[->, shorten >=1pt] (Hidden2-1) -- node [midway] {$1.00$} (Output); 
\draw[->, shorten >=1pt] (6,6) node [below] {$0.00$} --  (Hidden2-1); 
\draw[->, shorten >=1pt] (3,6) node [below] {$0.00$} --  (Hidden1-1); 
\end{tikzpicture}

We can now see, for example, that the initial slope of this function is what we’d like, but we have a problem.

%%itikz --temp-dir --tex-packages=tikz,pgfplots --tikz-libraries=arrows --implicit-standalone
\begin{tikzpicture}[scale=1.5]
\begin{axis}[grid,ymin=-2,ymax=2,ytick={-2,-1,...,2},xmin=0,xmax=1]
\addplot[color=blue,thick,samples=1000]{max(max(6*x,0),0)};
\addplot[color=green,samples=1000,domain=0:1]{sin(deg(2*3.14*x))};
\end{axis}
\end{tikzpicture}

Currently, this function never ends because this neuron pair never deactivates. We can visually see where we’d like the deactivation to occur. It’s where the red fitment line diverges from our green sine wave. So now, while we have the correct slope, we need to set this spot as our deactivation point. To do that, we start by increasing the bias for the second neuron of the hidden layer to \(0.70\).

%%itikz --temp-dir --tex-packages=tikz --tikz-libraries=arrows --implicit-standalone
\begin{tikzpicture}

\node[circle, 
    minimum size = 15mm,
    fill=red!30
    ] (Input) at (0,0) {\large $x_1$};

\foreach \i in {1,2,...,8}
{
    \node[circle, 
        minimum size = 15mm,
        fill=blue!50,
        yshift=90 mm
        ] (Hidden1-\i) at (3.0,-\i * 2) {\large $h_\i^{(1)}$};
        
}
\foreach \i in {1,2,...,8}
{
    \node[circle, 
        minimum size = 15mm,
        fill=blue!50,
        yshift=90 mm
        ] (Hidden2-\i) at (6.0,-\i * 2) {\large $h_\i^{(2)}$};
        
}

\node[circle, 
    minimum size = 15mm,
    fill=red!30
    ] (Output) at (9,0) {\large $\hat{y}_1$};

% Connect neurons In-Hidden1
\foreach \j in {2,...,8}
{
    \draw[->, shorten >=1pt] (Input) -- (Hidden1-\j);   
}
% Connect neurons Hidden1-Hidden2
\foreach \i in {2,...,8}
{
    
        \draw[->, shorten >=1pt] (Hidden1-\i) -- (Hidden2-\i);   
    
}

\foreach \i in {2,...,8}
{
    
        \draw[->, shorten >=1pt] (Hidden2-\i) -- (Output);   
}
\draw[->, shorten >=1pt] (Input) -- node [midway] {$6.00$} (Hidden1-1);   
\draw[->, shorten >=1pt] (Hidden1-1) -- node [midway,above] {$1.00$} (Hidden2-1); 
\draw[->, shorten >=1pt] (Hidden2-1) -- node [midway] {$1.00$} (Output); 
\draw[->, shorten >=1pt] (6,6) node [below] {$0.70$} --  (Hidden2-1); 
\draw[->, shorten >=1pt] (3,6) node [below] {$0.00$} --  (Hidden1-1); 
\end{tikzpicture}

Recall, that this offsets the overall function vertically:

%%itikz --temp-dir --tex-packages=tikz,pgfplots --tikz-libraries=arrows --implicit-standalone
\begin{tikzpicture}[scale=1.5]
\begin{axis}[grid,ymin=-2,ymax=2,ytick={-2,-1,...,2},xmin=0,xmax=1]
\addplot[color=blue,thick,samples=1000]{max(max(6*x,0)+0.70,0)};
\addplot[color=green,samples=1000,domain=0:1]{sin(deg(2*3.14*x))};
\end{axis}
\end{tikzpicture}

Now, we can set the weight for the second neuron to \(-1\), causing a deactivation point to occur, atleast horizontally, where we want it.

%%itikz --temp-dir --tex-packages=tikz --tikz-libraries=arrows --implicit-standalone
\begin{tikzpicture}

\node[circle, 
    minimum size = 15mm,
    fill=red!30
    ] (Input) at (0,0) {\large $x_1$};

\foreach \i in {1,2,...,8}
{
    \node[circle, 
        minimum size = 15mm,
        fill=blue!50,
        yshift=90 mm
        ] (Hidden1-\i) at (3.0,-\i * 2) {\large $h_\i^{(1)}$};
        
}
\foreach \i in {1,2,...,8}
{
    \node[circle, 
        minimum size = 15mm,
        fill=blue!50,
        yshift=90 mm
        ] (Hidden2-\i) at (6.0,-\i * 2) {\large $h_\i^{(2)}$};
        
}

\node[circle, 
    minimum size = 15mm,
    fill=red!30
    ] (Output) at (9,0) {\large $\hat{y}_1$};

% Connect neurons In-Hidden1
\foreach \j in {2,...,8}
{
    \draw[->, shorten >=1pt] (Input) -- (Hidden1-\j);   
}
% Connect neurons Hidden1-Hidden2
\foreach \i in {2,...,8}
{
    
        \draw[->, shorten >=1pt] (Hidden1-\i) -- (Hidden2-\i);   
    
}

\foreach \i in {2,...,8}
{
    
        \draw[->, shorten >=1pt] (Hidden2-\i) -- (Output);   
}
\draw[->, shorten >=1pt] (Input) -- node [midway] {$6.00$} (Hidden1-1);   
\draw[->, shorten >=1pt] (Hidden1-1) -- node [midway,above] {$-1.00$} (Hidden2-1); 
\draw[->, shorten >=1pt] (Hidden2-1) -- node [midway] {$1.00$} (Output); 
\draw[->, shorten >=1pt] (6,6) node [below] {$0.70$} --  (Hidden2-1); 
\draw[->, shorten >=1pt] (3,6) node [below] {$0.00$} --  (Hidden1-1); 
\end{tikzpicture}

We get:

%%itikz --temp-dir --tex-packages=tikz,pgfplots --tikz-libraries=arrows --implicit-standalone
\begin{tikzpicture}[scale=1.5]
\begin{axis}[grid,ymin=-2,ymax=2,ytick={-2,-1,...,2},xmin=0,xmax=1]
\addplot[color=blue,thick,samples=1000]{max(-max(6*x,0)+0.70,0)};
\addplot[color=green,samples=1000,domain=0:1]{sin(deg(2*3.14*x))};
\end{axis}
\end{tikzpicture}

Now, we’d like to flip this slope back. How might we flip the output of these two neurons?

%%itikz --temp-dir --tex-packages=tikz --tikz-libraries=arrows --implicit-standalone
\begin{tikzpicture}

\node[circle, 
    minimum size = 15mm,
    fill=red!30
    ] (Input) at (0,0) {\large $x_1$};

\foreach \i in {1,2,...,8}
{
    \node[circle, 
        minimum size = 15mm,
        fill=blue!50,
        yshift=90 mm
        ] (Hidden1-\i) at (3.0,-\i * 2) {\large $h_\i^{(1)}$};
        
}
\foreach \i in {1,2,...,8}
{
    \node[circle, 
        minimum size = 15mm,
        fill=blue!50,
        yshift=90 mm
        ] (Hidden2-\i) at (6.0,-\i * 2) {\large $h_\i^{(2)}$};
        
}

\node[circle, 
    minimum size = 15mm,
    fill=red!30
    ] (Output) at (9,0) {\large $\hat{y}_1$};

% Connect neurons In-Hidden1
\foreach \j in {2,...,8}
{
    \draw[->, shorten >=1pt] (Input) -- (Hidden1-\j);   
}
% Connect neurons Hidden1-Hidden2
\foreach \i in {2,...,8}
{
    
        \draw[->, shorten >=1pt] (Hidden1-\i) -- (Hidden2-\i);   
    
}

\foreach \i in {2,...,8}
{
    
        \draw[->, shorten >=1pt] (Hidden2-\i) -- (Output);   
}
\draw[->, shorten >=1pt] (Input) -- node [midway] {$6.00$} (Hidden1-1);   
\draw[->, shorten >=1pt] (Hidden1-1) -- node [midway,above] {$-1.00$} (Hidden2-1); 
\draw[->, shorten >=1pt] (Hidden2-1) -- node [midway] {$-1.00$} (Output); 
\draw[->, shorten >=1pt] (6,6) node [below] {$0.70$} --  (Hidden2-1); 
\draw[->, shorten >=1pt] (3,6) node [below] {$0.00$} --  (Hidden1-1); 
\end{tikzpicture}

It seems like we can take the weights of the connection to the output neuron, which is currently \(1.0\) and just flip it to a \(-1\), and that flips the function:

%%itikz --temp-dir --tex-packages=tikz,pgfplots --tikz-libraries=arrows --implicit-standalone
\begin{tikzpicture}[scale=1.5]
\begin{axis}[grid,ymin=-2,ymax=2,ytick={-2,-1,...,2},xmin=0,xmax=1]
\addplot[color=blue,thick,samples=1000]{-max(-max(6*x,0)+0.70,0)};
\addplot[color=green,samples=1000,domain=0:1]{sin(deg(2*3.14*x))};
\end{axis}
\end{tikzpicture}

We’re certainly getting closer to making this first section fit how we want. Now, all we need to do is offset this up a bit. For this hand-optimized example, we’re going to use the first \(7\) pairs of neurons in the hidden layers to create the sine wave’s shape.

%%itikz --temp-dir --tex-packages=tikz --tikz-libraries=arrows --implicit-standalone
\begin{tikzpicture}

\node[circle, 
    minimum size = 15mm,
    fill=red!30
    ] (Input) at (0,0) {\large $x_1$};

\foreach \i in {1,2,...,8}
{
    \node[circle, 
        minimum size = 15mm,
        fill=blue!50,
        yshift=90 mm
        ] (Hidden1-\i) at (3.0,-\i * 2) {\large $h_\i^{(1)}$};
        
}
\foreach \i in {1,2,...,8}
{
    \node[circle, 
        minimum size = 15mm,
        fill=blue!50,
        yshift=90 mm
        ] (Hidden2-\i) at (6.0,-\i * 2) {\large $h_\i^{(2)}$};
        
}

\node[circle, 
    minimum size = 15mm,
    fill=red!30
    ] (Output) at (9,0) {\large $\hat{y}_1$};

% Connect neurons In-Hidden1
\foreach \j in {2,...,7}
{
    \draw[->, shorten >=1pt] (Input) -- (Hidden1-\j);   
}
% Connect neurons Hidden1-Hidden2
\foreach \i in {2,...,7}
{
    
        \draw[->, shorten >=1pt] (Hidden1-\i) -- (Hidden2-\i);   
    
}

\foreach \i in {2,...,7}
{
    
        \draw[->, shorten >=1pt] (Hidden2-\i) -- (Output);   
}
\draw[->, shorten >=1pt] (Input) -- node [midway] {$6.00$} (Hidden1-1);   
\draw[->, shorten >=1pt] (Hidden1-1) -- node [midway,above] {$-1.00$} (Hidden2-1); 
\draw[->, shorten >=1pt] (Hidden2-1) -- node [midway] {$-1.00$} (Output); 
\draw[->, shorten >=1pt] (6,6) node [below] {$0.70$} --  (Hidden2-1); 
\draw[->, shorten >=1pt] (3,6) node [below] {$0.00$} --  (Hidden1-1); 

\draw[->, shorten >=1pt] (Input) -- node [midway] {$0.00$} (Hidden1-8); 
\draw[->, shorten >=1pt] (3,-9) node [below] {$0.00$} --  (Hidden1-8); 
\draw[->, shorten >=1pt] (Hidden1-8) -- node [midway,above] {$0.00$} (Hidden2-8); 
\draw[->, shorten >=1pt] (6,-9) node [below] {$1.00$} --  (Hidden2-8); 
\draw[->, shorten >=1pt] (Hidden2-8) -- node [midway] {$0.70$} (Output); 
\end{tikzpicture}

If we set the bias of the second neuron in the bottom pair to \(1.0\) and the weight to the output neuron to \(0.70\), we can vertically shift the line like so:

%%itikz --temp-dir --tex-packages=tikz,pgfplots --tikz-libraries=arrows --implicit-standalone
\begin{tikzpicture}[scale=1.5]
\begin{axis}[grid,ymin=-2,ymax=2,ytick={-2,-1,...,2},xmin=0,xmax=1]
\addplot[color=blue,thick,samples=1000]{-max(-max(6*x,0)+0.70,0))+0.70};
\addplot[color=green,samples=1000,domain=0:1]{sin(deg(2*3.14*x))};
\end{axis}
\end{tikzpicture}

At this point, we have completed the first section with an “area of effect” being the first upward section of the sine wave. We can start on the next section that we wish to do. We can start on the next section that we wish to do. We can start by setting all weights for this second pair of neurons to \(1\) including the output neuron.

%%itikz --temp-dir --tex-packages=tikz --tikz-libraries=arrows --implicit-standalone
\begin{tikzpicture}

\node[circle, 
    minimum size = 15mm,
    fill=red!30
    ] (Input) at (0,0) {\large $x_1$};

\foreach \i in {1,2,...,8}
{
    \node[circle, 
        minimum size = 15mm,
        fill=blue!50,
        yshift=90 mm
        ] (Hidden1-\i) at (3.0,-\i * 2) {\large $h_\i^{(1)}$};
        
}
\foreach \i in {1,2,...,8}
{
    \node[circle, 
        minimum size = 15mm,
        fill=blue!50,
        yshift=90 mm
        ] (Hidden2-\i) at (6.0,-\i * 2) {\large $h_\i^{(2)}$};
        
}

\node[circle, 
    minimum size = 15mm,
    fill=red!30
    ] (Output) at (9,0) {\large $\hat{y}_1$};

% Connect neurons In-Hidden1
\foreach \j in {3,...,7}
{
    \draw[->, shorten >=1pt] (Input) -- (Hidden1-\j);   
}
% Connect neurons Hidden1-Hidden2
\foreach \i in {3,...,7}
{
    
        \draw[->, shorten >=1pt] (Hidden1-\i) -- (Hidden2-\i);   
    
}

\foreach \i in {3,...,7}
{
    
        \draw[->, shorten >=1pt] (Hidden2-\i) -- (Output);   
}
\draw[->, shorten >=1pt] (Input) -- node [midway] {$6.00$} (Hidden1-1);   
\draw[->, shorten >=1pt] (Hidden1-1) -- node [midway,above] {$-1.00$} (Hidden2-1); 
\draw[->, shorten >=1pt] (Hidden2-1) -- node [midway] {$-1.00$} (Output); 
\draw[->, shorten >=1pt] (6,6) node [below] {$0.70$} --  (Hidden2-1); 
\draw[->, shorten >=1pt] (3,6) node [below] {$0.00$} --  (Hidden1-1); 

\draw[->, shorten >=1pt] (Input) -- node [midway] {$0.00$} (Hidden1-8); 
\draw[->, shorten >=1pt] (3,-9) node [below] {$0.00$} --  (Hidden1-8); 
\draw[->, shorten >=1pt] (Hidden1-8) -- node [midway,above] {$0.00$} (Hidden2-8); 
\draw[->, shorten >=1pt] (6,-9) node [below] {$1.00$} --  (Hidden2-8); 
\draw[->, shorten >=1pt] (Hidden2-8) -- node [midway] {$0.70$} (Output); 

\draw[->, shorten >=1pt] (Input) -- node [midway] {$1.00$} (Hidden1-2); 
\draw[->, shorten >=1pt] (3,4) node [below] {$0.00$} --  (Hidden1-2); 
\draw[->, shorten >=1pt] (Hidden1-2) -- node [midway,above] {$1.00$} (Hidden2-2); 
\draw[->, shorten >=1pt] (6,4) node [below] {$0.00$} --  (Hidden2-2); 
\draw[->, shorten >=1pt] (Hidden2-2) -- node [midway] {$1.00$} (Output); 
\end{tikzpicture}

At this point, this second pair of neurons activation is beginning too soon, which is impacting the area of effect of the top pair we already aligned.

%%itikz --temp-dir --tex-packages=tikz,pgfplots --tikz-libraries=arrows --implicit-standalone
\begin{tikzpicture}[scale=1.5]
\begin{axis}[grid,ymin=-2,ymax=2,ytick={-2,-1,...,2},xmin=0,xmax=1]
\addplot[color=blue,thick,samples=1000]{-max(-max(6*x,0)+0.70,0))+0.70+max(max(x,0),0)};
\addplot[color=green,samples=1000,domain=0:1]{sin(deg(2*3.14*x))};
\end{axis}
\end{tikzpicture}

To fix this, we want this second pair to start influencing the output where the first pair deactivates, so we want to adjust the function horizontally. As you can recall from earlier, we adjust the first neuron’s bias in this neuron pair to achieve this. Also, to modify the slope, we’ll set the weight coming into that first neuron for the second pair, setting it to \(3.50\).

%%itikz --temp-dir --tex-packages=tikz --tikz-libraries=arrows --implicit-standalone
\begin{tikzpicture}

\node[circle, 
    minimum size = 15mm,
    fill=red!30
    ] (Input) at (0,0) {\large $x_1$};

\foreach \i in {1,2,...,8}
{
    \node[circle, 
        minimum size = 15mm,
        fill=blue!50,
        yshift=90 mm
        ] (Hidden1-\i) at (3.0,-\i * 2) {\large $h_\i^{(1)}$};
        
}
\foreach \i in {1,2,...,8}
{
    \node[circle, 
        minimum size = 15mm,
        fill=blue!50,
        yshift=90 mm
        ] (Hidden2-\i) at (6.0,-\i * 2) {\large $h_\i^{(2)}$};
        
}

\node[circle, 
    minimum size = 15mm,
    fill=red!30
    ] (Output) at (9,0) {\large $\hat{y}_1$};

% Connect neurons In-Hidden1
\foreach \j in {3,...,7}
{
    \draw[->, shorten >=1pt] (Input) -- (Hidden1-\j);   
}
% Connect neurons Hidden1-Hidden2
\foreach \i in {3,...,7}
{
    
        \draw[->, shorten >=1pt] (Hidden1-\i) -- (Hidden2-\i);   
    
}

\foreach \i in {3,...,7}
{
    
        \draw[->, shorten >=1pt] (Hidden2-\i) -- (Output);   
}
\draw[->, shorten >=1pt] (Input) -- node [midway] {$6.00$} (Hidden1-1);   
\draw[->, shorten >=1pt] (Hidden1-1) -- node [midway,above] {$-1.00$} (Hidden2-1); 
\draw[->, shorten >=1pt] (Hidden2-1) -- node [midway] {$-1.00$} (Output); 
\draw[->, shorten >=1pt] (6,6) node [below] {$0.70$} --  (Hidden2-1); 
\draw[->, shorten >=1pt] (3,6) node [below] {$0.00$} --  (Hidden1-1); 

\draw[->, shorten >=1pt] (Input) -- node [midway] {$0.00$} (Hidden1-8); 
\draw[->, shorten >=1pt] (3,-9) node [below] {$0.00$} --  (Hidden1-8); 
\draw[->, shorten >=1pt] (Hidden1-8) -- node [midway,above] {$0.00$} (Hidden2-8); 
\draw[->, shorten >=1pt] (6,-9) node [below] {$1.00$} --  (Hidden2-8); 
\draw[->, shorten >=1pt] (Hidden2-8) -- node [midway] {$0.70$} (Output); 

\draw[->, shorten >=1pt] (Input) -- node [midway] {$3.50$} (Hidden1-2); 
\draw[->, shorten >=1pt] (3,4) node [below] {$-0.42$} --  (Hidden1-2); 
\draw[->, shorten >=1pt] (Hidden1-2) -- node [midway,above] {$1.00$} (Hidden2-2); 
\draw[->, shorten >=1pt] (6,4) node [below] {$0.00$} --  (Hidden2-2); 
\draw[->, shorten >=1pt] (Hidden2-2) -- node [midway] {$1.00$} (Output); 
\end{tikzpicture}

After these adjustments:

%%itikz --temp-dir --tex-packages=tikz,pgfplots --tikz-libraries=arrows --implicit-standalone
\begin{tikzpicture}[scale=1.5]
\begin{axis}[grid,ymin=-2,ymax=2,ytick={-2,-1,...,2},xmin=0,xmax=1]
\addplot[color=blue,thick,samples=1000]{-max(-max(6*x,0)+0.70,0))+0.70+max(max(3.50*x - 0.42,0),0)};
\addplot[color=green,samples=1000,domain=0:1]{sin(deg(2*3.14*x))};
\end{axis}
\end{tikzpicture}

We will now use the same methodology as we did with the first pair of neurons to set the deactivation point. We set the weight for the second neuron in the hidden layer pair to \(-1.00\) and the bias to \(0.27\).

%%itikz --temp-dir --tex-packages=tikz --tikz-libraries=arrows --implicit-standalone
\begin{tikzpicture}

\node[circle, 
    minimum size = 15mm,
    fill=red!30
    ] (Input) at (0,0) {\large $x_1$};

\foreach \i in {1,2,...,8}
{
    \node[circle, 
        minimum size = 15mm,
        fill=blue!50,
        yshift=90 mm
        ] (Hidden1-\i) at (3.0,-\i * 2) {\large $h_\i^{(1)}$};
        
}
\foreach \i in {1,2,...,8}
{
    \node[circle, 
        minimum size = 15mm,
        fill=blue!50,
        yshift=90 mm
        ] (Hidden2-\i) at (6.0,-\i * 2) {\large $h_\i^{(2)}$};
        
}

\node[circle, 
    minimum size = 15mm,
    fill=red!30
    ] (Output) at (9,0) {\large $\hat{y}_1$};

% Connect neurons In-Hidden1
\foreach \j in {3,...,7}
{
    \draw[->, shorten >=1pt] (Input) -- (Hidden1-\j);   
}
% Connect neurons Hidden1-Hidden2
\foreach \i in {3,...,7}
{
    
        \draw[->, shorten >=1pt] (Hidden1-\i) -- (Hidden2-\i);   
    
}

\foreach \i in {3,...,7}
{
    
        \draw[->, shorten >=1pt] (Hidden2-\i) -- (Output);   
}
\draw[->, shorten >=1pt] (Input) -- node [midway] {$6.00$} (Hidden1-1);   
\draw[->, shorten >=1pt] (Hidden1-1) -- node [midway,above] {$-1.00$} (Hidden2-1); 
\draw[->, shorten >=1pt] (Hidden2-1) -- node [midway] {$-1.00$} (Output); 
\draw[->, shorten >=1pt] (6,6) node [below] {$0.70$} --  (Hidden2-1); 
\draw[->, shorten >=1pt] (3,6) node [below] {$0.00$} --  (Hidden1-1); 

\draw[->, shorten >=1pt] (Input) -- node [midway] {$0.00$} (Hidden1-8); 
\draw[->, shorten >=1pt] (3,-9) node [below] {$0.00$} --  (Hidden1-8); 
\draw[->, shorten >=1pt] (Hidden1-8) -- node [midway,above] {$0.00$} (Hidden2-8); 
\draw[->, shorten >=1pt] (6,-9) node [below] {$1.00$} --  (Hidden2-8); 
\draw[->, shorten >=1pt] (Hidden2-8) -- node [midway] {$0.70$} (Output); 

\draw[->, shorten >=1pt] (Input) -- node [midway] {$3.50$} (Hidden1-2); 
\draw[->, shorten >=1pt] (3,4) node [below] {$-0.42$} --  (Hidden1-2); 
\draw[->, shorten >=1pt] (Hidden1-2) -- node [midway,above] {$-1.00$} (Hidden2-2); 
\draw[->, shorten >=1pt] (6,4) node [below] {$0.27$} --  (Hidden2-2); 
\draw[->, shorten >=1pt] (Hidden2-2) -- node [midway] {$1.00$} (Output); 
\end{tikzpicture}

This results in:

%%itikz --temp-dir --tex-packages=tikz,pgfplots --tikz-libraries=arrows --implicit-standalone
\begin{tikzpicture}[scale=1.5]
\begin{axis}[grid,ymin=-2,ymax=2,ytick={-2,-1,...,2},xmin=0,xmax=1]
\addplot[color=blue,thick,samples=1000]{-max(-max(6*x,0)+0.70,0))+0.70+max(-max(3.50*x - 0.42,0)+0.27,0)};
\addplot[color=green,samples=1000,domain=0:1]{sin(deg(2*3.14*x))};
\end{axis}
\end{tikzpicture}

Then, we can flip this section’s function again the same way we did with the first one, by setting the weight to the output neuron from \(1.0\) to \(-1.0\).

%%itikz --temp-dir --tex-packages=tikz --tikz-libraries=arrows --implicit-standalone
\begin{tikzpicture}

\node[circle, 
    minimum size = 15mm,
    fill=red!30
    ] (Input) at (0,0) {\large $x_1$};

\foreach \i in {1,2,...,8}
{
    \node[circle, 
        minimum size = 15mm,
        fill=blue!50,
        yshift=90 mm
        ] (Hidden1-\i) at (3.0,-\i * 2) {\large $h_\i^{(1)}$};
        
}
\foreach \i in {1,2,...,8}
{
    \node[circle, 
        minimum size = 15mm,
        fill=blue!50,
        yshift=90 mm
        ] (Hidden2-\i) at (6.0,-\i * 2) {\large $h_\i^{(2)}$};
        
}

\node[circle, 
    minimum size = 15mm,
    fill=red!30
    ] (Output) at (9,0) {\large $\hat{y}_1$};

% Connect neurons In-Hidden1
\foreach \j in {3,...,7}
{
    \draw[->, shorten >=1pt] (Input) -- (Hidden1-\j);   
}
% Connect neurons Hidden1-Hidden2
\foreach \i in {3,...,7}
{
    
        \draw[->, shorten >=1pt] (Hidden1-\i) -- (Hidden2-\i);   
    
}

\foreach \i in {3,...,7}
{
    
        \draw[->, shorten >=1pt] (Hidden2-\i) -- (Output);   
}
\draw[->, shorten >=1pt] (Input) -- node [midway] {$6.00$} (Hidden1-1);   
\draw[->, shorten >=1pt] (Hidden1-1) -- node [midway,above] {$-1.00$} (Hidden2-1); 
\draw[->, shorten >=1pt] (Hidden2-1) -- node [midway] {$-1.00$} (Output); 
\draw[->, shorten >=1pt] (6,6) node [below] {$0.70$} --  (Hidden2-1); 
\draw[->, shorten >=1pt] (3,6) node [below] {$0.00$} --  (Hidden1-1); 

\draw[->, shorten >=1pt] (Input) -- node [midway] {$0.00$} (Hidden1-8); 
\draw[->, shorten >=1pt] (3,-9) node [below] {$0.00$} --  (Hidden1-8); 
\draw[->, shorten >=1pt] (Hidden1-8) -- node [midway,above] {$0.00$} (Hidden2-8); 
\draw[->, shorten >=1pt] (6,-9) node [below] {$1.00$} --  (Hidden2-8); 
\draw[->, shorten >=1pt] (Hidden2-8) -- node [midway] {$0.70$} (Output); 

\draw[->, shorten >=1pt] (Input) -- node [midway] {$3.50$} (Hidden1-2); 
\draw[->, shorten >=1pt] (3,4) node [below] {$-0.42$} --  (Hidden1-2); 
\draw[->, shorten >=1pt] (Hidden1-2) -- node [midway,above] {$-1.00$} (Hidden2-2); 
\draw[->, shorten >=1pt] (6,4) node [below] {$0.27$} --  (Hidden2-2); 
\draw[->, shorten >=1pt] (Hidden2-2) -- node [midway] {$-1.00$} (Output); 
\end{tikzpicture}

Consequently, we have:

%%itikz --temp-dir --tex-packages=tikz,pgfplots --tikz-libraries=arrows --implicit-standalone
\begin{tikzpicture}[scale=1.5]
\begin{axis}[grid,ymin=-2,ymax=2,ytick={-2,-1,...,2},xmin=0,xmax=1]
\addplot[color=blue,thick,samples=1000]{-max(-max(6*x,0)+0.70,0))+0.70-max(-max(3.50*x - 0.42,0)+0.27,0)};
\addplot[color=green,samples=1000,domain=0:1]{sin(deg(2*3.14*x))};
\end{axis}
\end{tikzpicture}

And again, just like the first pair, we use the bottom pair to fix the vertical offset.

%%itikz --temp-dir --tex-packages=tikz --tikz-libraries=arrows --implicit-standalone
\begin{tikzpicture}

\node[circle, 
    minimum size = 15mm,
    fill=red!30
    ] (Input) at (0,0) {\large $x_1$};

\foreach \i in {1,2,...,8}
{
    \node[circle, 
        minimum size = 15mm,
        fill=blue!50,
        yshift=90 mm
        ] (Hidden1-\i) at (3.0,-\i * 2) {\large $h_\i^{(1)}$};
        
}
\foreach \i in {1,2,...,8}
{
    \node[circle, 
        minimum size = 15mm,
        fill=blue!50,
        yshift=90 mm
        ] (Hidden2-\i) at (6.0,-\i * 2) {\large $h_\i^{(2)}$};
        
}

\node[circle, 
    minimum size = 15mm,
    fill=red!30
    ] (Output) at (9,0) {\large $\hat{y}_1$};

% Connect neurons In-Hidden1
\foreach \j in {3,...,7}
{
    \draw[->, shorten >=1pt] (Input) -- (Hidden1-\j);   
}
% Connect neurons Hidden1-Hidden2
\foreach \i in {3,...,7}
{
    
        \draw[->, shorten >=1pt] (Hidden1-\i) -- (Hidden2-\i);   
    
}

\foreach \i in {3,...,7}
{
    
        \draw[->, shorten >=1pt] (Hidden2-\i) -- (Output);   
}
\draw[->, shorten >=1pt] (Input) -- node [midway] {$6.00$} (Hidden1-1);   
\draw[->, shorten >=1pt] (Hidden1-1) -- node [midway,above] {$-1.00$} (Hidden2-1); 
\draw[->, shorten >=1pt] (Hidden2-1) -- node [midway] {$-1.00$} (Output); 
\draw[->, shorten >=1pt] (6,6) node [below] {$0.70$} --  (Hidden2-1); 
\draw[->, shorten >=1pt] (3,6) node [below] {$0.00$} --  (Hidden1-1); 

\draw[->, shorten >=1pt] (Input) -- node [midway] {$0.00$} (Hidden1-8); 
\draw[->, shorten >=1pt] (3,-9) node [below] {$0.00$} --  (Hidden1-8); 
\draw[->, shorten >=1pt] (Hidden1-8) -- node [midway,above] {$0.00$} (Hidden2-8); 
\draw[->, shorten >=1pt] (6,-9) node [below] {$1.00$} --  (Hidden2-8); 
\draw[->, shorten >=1pt] (Hidden2-8) -- node [midway] {$0.97$} (Output); 

\draw[->, shorten >=1pt] (Input) -- node [midway] {$3.50$} (Hidden1-2); 
\draw[->, shorten >=1pt] (3,4) node [below] {$-0.42$} --  (Hidden1-2); 
\draw[->, shorten >=1pt] (Hidden1-2) -- node [midway,above] {$-1.00$} (Hidden2-2); 
\draw[->, shorten >=1pt] (6,4) node [below] {$0.27$} --  (Hidden2-2); 
\draw[->, shorten >=1pt] (Hidden2-2) -- node [midway] {$-1.00$} (Output); 
\end{tikzpicture}

We get:

%%itikz --temp-dir --tex-packages=tikz,pgfplots --tikz-libraries=arrows --implicit-standalone
\begin{tikzpicture}[scale=1.5]
\begin{axis}[grid,ymin=-2,ymax=2,ytick={-2,-1,...,2},xmin=0,xmax=1]
\addplot[color=blue,thick,samples=1000]{-max(-max(6*x,0)+0.70,0))+0.97-max(-max(3.50*x - 0.42,0)+0.27,0)};
\addplot[color=green,samples=1000,domain=0:1]{sin(deg(2*3.14*x))};
\end{axis}
\end{tikzpicture}

We then just continue this methodology. It should begin to make more sense to you now, how more neurons can enable more unique areas of effect, why we need two or more hidden layers, and why we need nonlinear activation functions to map nonlinear problems.

We can write a ReLUActivation class to represent the ReLU activation function:

class ReLUActivation:

    # Forward pass
    def forward(self, inputs):
        # Calculate output values from the inputs
        self.output = np.maximum(0, inputs)

Let’s apply this activation function to the DenseLayer’s outputs in our code:

from nnfs.datasets import spiral_data
import numpy as np

# Create dataset
X, y = spiral_data(samples=100, classes=3)

# Create Dense layer with 2 input features and 3 output values
dense1 = DenseLayer(2, 3)

# Create ReLU activation function (to be used with the DenseLayer)
activation1 = ReLUActivation()

# Make a forward pass of our training data through this layer
dense1.forward(X)

# Forward pass through our activation function
# Takes in output from the previous layer
activation1.forward(dense1.output)

# Let's see output of the first few samples
print(activation1.output[:5])

[[0.0000000e+00 0.0000000e+00 0.0000000e+00]
 [1.3520580e-04 1.8173116e-05 0.0000000e+00]
 [2.3245417e-04 0.0000000e+00 0.0000000e+00]
 [3.8226307e-04 0.0000000e+00 0.0000000e+00]
 [5.7436468e-04 0.0000000e+00 0.0000000e+00]]

As we can see, negative values have been clipped (modified to zero). That’s all there is to the rectified linear activation function used in the hidden layer. Let’s talk about the activation function that we are going to use on the output of the last layer.

The Softmax Activation function

In our case, we’re looking to get this model to be a classifier, so we want an activation function meant for classification. One of these is the softmax activation function. First, why are we bothering with another activation function? It just depends on what our overall goals are.

The rectified linear unit is unbounded, not normalized with other units and exclusive. “Not normalized” implies the values can be anything, an output of [12,99,318] is without context, and exclusive means each output is independent of others. To address this lack of context, the softmax activation function on the output data can take in non-normalized, or uncalibrated, inputs and produce a normalized distribution of probabilities for our classes. In the case of classification, what we want to see is a prediction of which class the network thinks the input represents. This distribution returned by the softmax activation function represents confidence scores in our overarching algorithm/program that uses this network. For example, if our network has a confidence distirbution for two classes \([0.45,0.55]\), the prediction is the \(2\)nd class, but the confidence in this prediction isn’t very high.

Maybe our program wouldn’t act in this case, since it’s not very confident.

The softmax function takes as input a vector of \(L\) real numbers and normalizes it into a probability distribution consisting of \(L\) probabilities proportional to the exponentials of the input numbers.

Definition. The standard(unit) softmax function \(\sigma:\mathbf{R}^L \to (0,1)^L\) takes a vector \(\mathbf{z}=(z_1,\ldots,z_l)\in\mathbf{R}^L\) and computes each component of the vector \(\sigma(\mathbf{z})\in(0,1)^L\) with:

\[\begin{align*} \sigma(\mathbf{z})_i = \frac{e^{z_{i}}}{\sum_{l=1}^{L}e^{z_{l}}} \end{align*}\]

That might look daunting, but it’s easy to follow. Suppose the example outputs from a neural network layer are:

layer_outputs = [4.80, 1.21, 2.385]

Then, the normalized values are:

import numpy as np

norm_values = np.exp(layer_outputs)/np.sum(np.exp(layer_outputs))
print(norm_values)

[0.89528266 0.02470831 0.08000903]

To train in batches, we need to convert this functionality to accept layer outputs in batches. Do this is easy:

layer_outputs = np.random.randn(100,3)
norm_values = np.exp(layer_outputs)/np.sum(np.exp(layer_outputs),axis=1,keepdims=True)

We can now write a SoftmaxActivation class as:

# Softmax activation
class SoftmaxActivation:

    # Forward pass
    def forward(self, inputs):
        exp_values = np.exp(inputs - np.max(inputs, axis=1, keepdims=True))
        probabilities = exp_values / np.sum(exp_values, axis=1, keepdims=True)
        self.output = probabilities

We also included a subtraction of the largest of the inputs before we do the exponentiation. This does not affect the output of the softmax function, since:

\[\begin{align*} \frac{e^{z_{i}-||\mathbf{z}||}}{\sum_{l=1}^{L}e^{z_{l}-||\mathbf{z}||}} = \frac{e^{-||\mathbf{z}||}\cdot e^{z_{i}}}{e^{-||\mathbf{z}||}\cdot \sum_{l=1}^{L}e^{z_{l}}} = \sigma(\mathbf{z})_i \end{align*}\]

There are two main pervasive challenges with neural networks : dead neurons and very large numbers (referred to as exploding values). Dead neurons and enormous numbers can wreak havoc down the line and render a network useless over time.

The output layer

Now, we can add another DenseLayer as the output layer, setting it to contain as many inputs as the previous layer outputs and as many outputs as our data includes classes. Then, we can apply the softmax function to the output of this new layer.

Full code upto this point

import numpy as np
import nnfs
from nnfs.datasets import spiral_data

class DenseLayer:

    def __init__(self, n_inputs, n_neurons):
        # Initialize all weights and biases
        self.weights = 0.01 * np.random.randn(n_inputs,n_neurons)
        self.biases = np.zeros((1,n_neurons))
    
    def forward(self, inputs):
        self.output = np.dot(inputs,self.weights) + self.biases

class ReLUActivation:

    # Forward pass
    def forward(self, inputs):
        self.output = np.maximum(inputs, 0)

class SoftmaxActivation:

    # Forward pass
    def forward(self,inputs):
        exp_values = np.exp(inputs - np.max(inputs, axis=1, keepdims=True))
        probabilities = exp_values / np.sum(exp_values, axis=1, keepdims=True)
        self.output = probabilities

# Create dataset
X, y = spiral_data(samples=100, classes=3)

# Create a DenseLayer with 2 input features and 3 neurons
dense1 = DenseLayer(2, 3)

# Create ReLU Activation (to be used with DenseLayer)
activation1 = ReLUActivation()

# Create a second DenseLayer with 3 input features and 3 output values
dense2 = DenseLayer(3, 3)

# Create Softmax activation to be used with the output layer
activation2 = SoftmaxActivation()

# Make a forward pass of our training data through this layer
dense1.forward(X)

# Make a forward pass through the activation function 
# It takes the output of the first dense layer
activation1.forward(dense1.output)

# Make a forward pass through the second DenseLayer
# It takes outputs of the activation function of the first layer
# as inputs
dense2.forward(activation1.output)

# Make a forward pass through activation function
# It takes outputs of the second dense layer
activation2.forward(dense2.output)

# Let's see output of the first few examples
print(activation2.output[:5])

[[0.33333334 0.33333334 0.33333334]
 [0.33333322 0.3333335  0.33333322]
 [0.3333332  0.3333332  0.3333336 ]
 [0.3333332  0.3333336  0.3333332 ]
 [0.33333287 0.33333436 0.33333275]]

We’ve completed what we need for forward-passing data through the model.

Our example model is currently random. To remedy this, we need a way to calculate how wrong the neural network is at current predictions and begin adjusting weights and biases to decrease error over time. Thus, our next step is to quantify how wrong the model is through what’s defined as a loss function.