Puzzles on discrete probability
Example 1 We flip a fair coin until we obtain our first heads. If the first heads occurs on the \(k\)-th flip, we are given \(k\) balls. We put them into 3 bins labeled 1, 2, and 3 at random. Find the probability that none of the three bins are empty.
Solution.
Let \(A_k\) be the event that the first head occurs on the \(k\)th flip. So, we are interested in the sequence \(\underbrace{T \ldots T}_{(k-1)\text{-tails}}H\). We have:
\[ \mathbb{P}(A_k) = \left(\frac{1}{2}\right)^{k-1} \cdot \frac{1}{2} = \frac{1}{2^k} \]
Example 2 Imagine you have \(4\) \(6\)-sided dice. What is the probability that you roll a different number on each die?
Solution.
\[ p = \frac{6\cdot 5 \cdot 4 \cdot 3}{6^4} \]
Example 3 What is the probability of flipping exactly \(5\) heads when flipping \(10\) fair coins?
Solution.
\[ P(k = 5) = {10 \choose 5} \frac{1}{2^{10}} \]
Example 4 Two players are at deuce in a tennis match — player \(1\) has \(60\) percent of winning the point and player \(2\) has \(40\) percent chance. What are the odds of player 1 winning?
Solution
When a game is at the 40-40 mark, a player still needs two clear points to win the game. We can quickly draw the following state diagram to represent the game (it is a discrete-time markov chain).
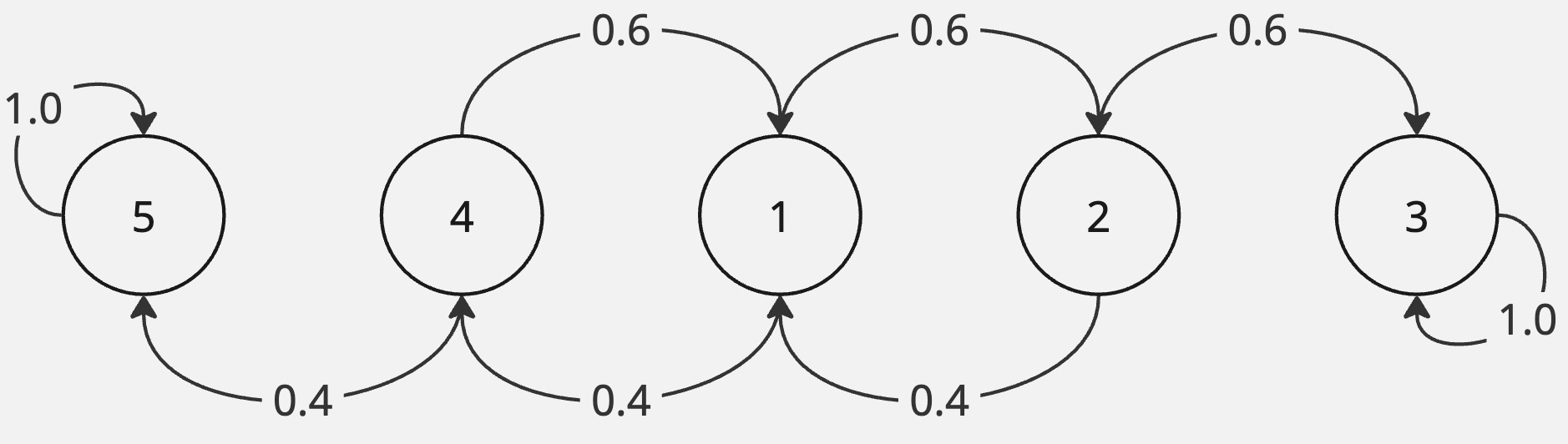
Let the state \(s_1 \stackrel{def}{=}\) the two players are 40-40. And the state \(s_3 \stackrel{def}{=}\) player \(1\) wins. The states \(3\) and \(5\) are absorbing states. Let \(p_{13}\) be the hitting probability of state \(3\) from state \(1\). We have:
\[ \begin{align*} p_{13} &= 0.6 p_{23} + 0.4 p_{43}\\ p_{23} &= 0.6 (1) + 0.4p_{13}\\ p_{43} &= 0.6p_{13} + 0.4(0) \end{align*} \]
It turns out that \(p_{13} = \frac{9}{13}\).
Example 5 You have a plate of spaghetti in front of you (no sauce!). You pick two ends and tie them together. Then you pick two more ends and tie them together. Continue until there are no free ends left. If there were \(n\) spaghettis originally, what is the probability that you now have a single giant loop consisting of all the spaghettis?
Let \(p_n\) be the probability of a single giant loop. \(n\) spaghettis have \(2n\) free ends. In each of the \(n\) trials, you pick \(2\) ends. At the start, the probability that you don’t tie a sphagetti to itself is
\[ \frac{2n}{2n} \cdot \frac{2n - 2}{2n - 1} = \frac{2n - 2}{2n - 1} \]
After the first draw, we have reduced the problem to \((n-1)\) spaghetti strands and \(2n-2\) free ends. So, the probability of no-loops is:
\[ p_n = \frac{2n - 2}{2n - 1} \cdot p_{n-1} \]
Extending this to \(k=(n-1)\) trials: \[ \begin{align*} p_n &= \frac{2n - 2}{2n - 1} \cdot \frac{2n-4}{2n-3} \cdots \frac{2}{1}\\ &= 2^{n-1} \frac{(n-1)!}{(2n-1)(2n-3)\cdots 1}\\ &= 2^{n-1} \frac{2^n n! (n-1)!}{(2n)(2n-1)(2n-2)(2n-3) \cdots 1}\\ &= 2^{2n-1} \frac{n! (n-1)!}{(2n)!}\\ \end{align*} \]
Example 6 An electronic safe has a three digit passcode. You are given three constraints regarding the code. Firstly, the code is not an odd number. Secondly, the code does not contain the number six. Lastly, one of the digits appears more than once. How many possible three digit entries satisfy these three requirements?
Solution.
Since it’s a \(3\)-digit electronic passcode to a safe, \(0\) is a valid first digit. The last digit must be one of \(0,2,4,8\). The first digit must be one of \(\{0,1,2,\ldots,5,7,8,9\}\). The middle digit must be must be one of \(\{0,1,2,\ldots,5,7,8,9\}\)
Case I. The first two digits are identical.
There are \(9 \times 1 \times 4 = 36\) such distinguishable codes.
Case II. The last two digits are identical.
There are \(9 \times 1 \times 4 = 36\) such distinguishable codes.
Case III. The first and the third digits are identical.
There are \(1 \times 9 \times 4 = 36\) such distinguishable codes.
Also, \(000\), \(222\), \(444\) and \(888\) have been overcounted \(3\) times. They should be accounted for only once. Hence, the number of possible three digit entries satisfying the above requirements are \(108 - 8 = 100\).
Example 7 Suppose we roll \(5\) standard fair dice and sum the faces of the largest \(3\) values showing. Find the probability that the sum is \(18\).
Solution.
To reach a sum of \(18\) on the largest three die faces, we must get atleast \(3\) sixes in \(5\) dice rolls.
Define success as getting a \(6\) on a die, \(p = \frac{1}{6}\), \(q=\frac{5}{6}\) and let \(X\) be the number of sixes in \(5\) die rolls.
\[ \begin{align*} P(X \ge 3) &= 1 - (P(X=0) + P(X=1) + P(X=2))\\ &= 1 - \left(\frac{5}{6}\right)^5 - {5 \choose 1} \left(\frac{1}{6}\right)\left(\frac{5}{6}\right)^4 - {5 \choose 2} \left(\frac{1}{6}\right)^2\left(\frac{5}{6}\right)^3\\ &= \frac{23}{648} \end{align*} \]
Example 8 Consider a \(2023 \times 2023\) grid. The grid squares from the middle row are shaded in. What is the probability that a randomly selected rectangle contains at least one shaded square?
Solution.
Let’s solve this puzzle for a smaller \(5 \times 5\) grid. A rectangle is always determined by a choice of a pair of vertical grid lines and a pair of horizonal grid lines.
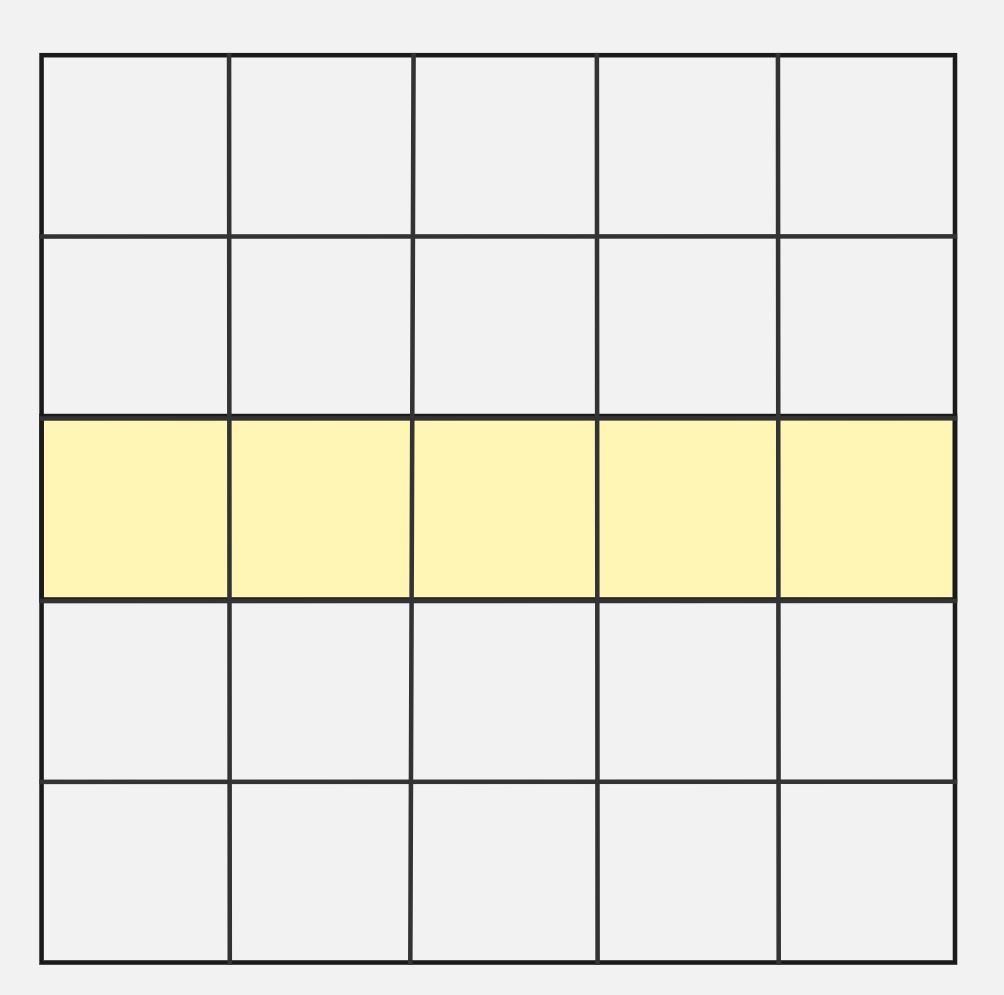
The number of horizontal and vertical grid lines are \(6\). So, the total number of rectangles are \({6 \choose 2} \times {6 \choose 2}\).
In order to pick rectangle that includes atleast one shaded square, one of the grid lines must chosen from the top \(3\) horizontal grid lines and the second grid line must be chosen from the bottom \(3\) horizontal grid lines. That yields \({3 \choose 1}^2\) pairs of horizontal grid lines. There are no restrictions on the vertical grid lines so there are \({6 \choose 2}\) pairs of vertical grid lines. Hence, the number of favorable rectangles are \(3^2 \times {6 \choose 2}\).
Generalizing, the desired probability for a \((2n-1) \times (2n-1)\) grid is:
\[ \begin{align*} p_{2n-1} &= \frac{n^2 \cdot {2n \choose 2}}{{2n \choose 2}^2} \\ &= \frac{n^2 }{{2n \choose 2}} \\ &= \frac{2n^2}{(2n)(2n-1)}\\ &= \frac{n}{2n-1} \end{align*} \]
So, \(p_{2023} = \frac{1012}{2023} \approx 0.5\).