Designing the `spsc_queue` data-structure

I would like to present my implementation for an SPSC lock-free queue in this blog-post.

%load_ext itikz

What makes an operation atomic?

When a programmer says that an operation is atomic, there are atleast two properties to which they might be referring:

Non-preemptible - The operation can’t be pre-empted in the middle (e.g. by another thread).
Synchronizable - The results of the operation can be made visible to other threads of execution in a controllable fashion.

Setup - How the queue works

Bounded size. The elements are stored in a fixed-length buffer.
Single-producer, Single-consumer applications.
Circular buffer. The head and tail cursors after reaching the maximum index of the buffer wrap around to the start of the buffer.

The spsc_queue type contains a fixed-length array - a buffer to store the elements of the queue and it also contains two indices into the array:

m_head - The index of the front element, if any.
m_tail - The index where a new element would be inserted at the back of the queue.

In an initially empty container, both the m_head and m_tail start at zero:

Show the code

%%itikz --temp-dir --tex-packages=tikz --tikz-libraries=arrows.meta --implicit-standalone
\begin{tikzpicture}[font=\small\ttfamily]
    \fill[white] (-2, 0.5) rectangle (8.5, -4.8);
    % Title
    \node[anchor=north] at (4, 0) {\textbf{SPSC Ring Buffer (Empty)}};
    
    % Index labels
    \node[anchor=east] at (-0.2, -1.5) {Index:};
    \foreach \i in {0,...,7} {
        \node at (\i, -1.5) {\i};
    }
    
    % Buffer cells
    \node[anchor=east] at (-0.2, -2.5) {Buffer:};
    \foreach \i in {0,...,7} {
        \draw (\i-0.4, -2.2) rectangle (\i+0.4, -2.8);
    }
    
    % Pointers
    \draw[->, thick] (0, -3.2) -- (0, -2.8);
    \node[anchor=north] at (0, -3.2) {m\_head = 0};
    \node[anchor=north] at (0, -3.6) {m\_tail = 0};
    
    % Status
    \node[anchor=north] at (4, -4.2) {Status: Empty (m\_head == m\_tail)};
\end{tikzpicture}

Then I have a spsc_queue::push_back() function that is used to append a new element to the queue. If the queue is not full, this operation should succeed, and it will go ahead and write a new element to the tail location and move the m_tail index forward.

For example, if do push_back(1) the queue looks something like this.

Show the code

%%itikz --temp-dir --tex-packages=tikz --tikz-libraries=arrows.meta --implicit-standalone
\begin{tikzpicture}[font=\small\ttfamily]
    \fill[white] (-2, 0.5) rectangle (8.5, -4.8);
    % Title
    \node[anchor=north] at (4, 0) {\textbf{SPSC Ring Buffer (1 element)}};
    
    % m_head pointer (above)
    \node[anchor=south] at (0, -0.8) {m\_head = 0};
    \draw[->, thick] (0, -1.0) -- (0, -1.4);
    
    % Index labels
    \node[anchor=east] at (-0.2, -1.5) {Index:};
    \foreach \i in {0,...,7} {
        \node at (\i, -1.5) {\i};
    }
    
    % Buffer cells
    \node[anchor=east] at (-0.2, -2.5) {Buffer:};
    \foreach \i in {0,...,7} {
        \draw (\i-0.4, -2.2) rectangle (\i+0.4, -2.8);
    }
    % Fill first cell
    \fill[lightgray!30] (-0.4, -2.2) rectangle (0.4, -2.8);
    \node at (0, -2.5) {1};
    
    % m_tail pointer (below)
    \draw[->, thick] (1, -3.2) -- (1, -2.8);
    \node[anchor=north] at (1, -3.2) {m\_tail = 1};
    
    % Status
    \node[anchor=north] at (4, -3.8) {Status: 1 element (m\_tail > m\_head)};
\end{tikzpicture}

Here’s the queue with a few more elements added:

Show the code

%%itikz --temp-dir --tex-packages=tikz --tikz-libraries=arrows.meta --implicit-standalone
\begin{tikzpicture}[font=\small\ttfamily]
    \fill[white] (-2, 0.5) rectangle (8.5, -4.8);
    % Title
    \node[anchor=north] at (4, 0) {\textbf{SPSC Ring Buffer (4 elements)}};
    
    % m_head pointer (above)
    \node[anchor=south] at (0, -0.8) {m\_head = 0};
    \draw[->, thick] (0, -1.0) -- (0, -1.4);
    
    % Index labels
    \node[anchor=east] at (-0.2, -1.5) {Index:};
    \foreach \i in {0,...,7} {
        \node at (\i, -1.5) {\i};
    }
    
    % Buffer cells
    \node[anchor=east] at (-0.2, -2.5) {Buffer:};
    \foreach \i in {0,...,7} {
        \draw (\i-0.4, -2.2) rectangle (\i+0.4, -2.8);
    }
    % Fill cells 0-3
    \fill[lightgray!30] (-0.4, -2.2) rectangle (0.4, -2.8);
    \fill[lightgray!30] (0.6, -2.2) rectangle (1.4, -2.8);
    \fill[lightgray!30] (1.6, -2.2) rectangle (2.4, -2.8);
    \fill[lightgray!30] (2.6, -2.2) rectangle (3.4, -2.8);
    \node at (0, -2.5) {1};
    \node at (1, -2.5) {2};
    \node at (2, -2.5) {3};
    \node at (3, -2.5) {5};
    
    % m_tail pointer (below)
    \draw[->, thick] (4, -3.2) -- (4, -2.8);
    \node[anchor=north] at (4, -3.2) {m\_tail = 4};
    
    % Status
    \node[anchor=north] at (4, -3.8) {Status: 4 elements (m\_tail > m\_head)};
\end{tikzpicture}

Once I have got some elements into the queue, I can go ahead and call the pop() function, which is going to try to read and remove the first element from the front of the queue.

If the queue isn’t empty, it :

Advances m_head thereby implicitly discard the element at the front of the queue

Show the code

%%itikz --temp-dir --tex-packages=tikz --tikz-libraries=arrows.meta --implicit-standalone
\begin{tikzpicture}[font=\small\ttfamily]
    \fill[white] (-2, 0.5) rectangle (8.5, -4.8);
    % Title
    \node[anchor=north] at (4, 0) {\textbf{SPSC Ring Buffer (3 elements)}};
    
    % m_head pointer (above)
    \node[anchor=south] at (1, -0.8) {m\_head = 1};
    \draw[->, thick] (1, -1.0) -- (1, -1.4);
    
    % Index labels
    \node[anchor=east] at (-0.2, -1.5) {Index:};
    \foreach \i in {0,...,7} {
        \node at (\i, -1.5) {\i};
    }
    
    % Buffer cells
    \node[anchor=east] at (-0.2, -2.5) {Buffer:};
    \foreach \i in {0,...,7} {
        \draw (\i-0.4, -2.2) rectangle (\i+0.4, -2.8);
    }
    % Fill cells 1-3
    \fill[lightgray!30] (0.6, -2.2) rectangle (1.4, -2.8);
    \fill[lightgray!30] (1.6, -2.2) rectangle (2.4, -2.8);
    \fill[lightgray!30] (2.6, -2.2) rectangle (3.4, -2.8);
    \node at (1, -2.5) {2};
    \node at (2, -2.5) {3};
    \node at (3, -2.5) {5};
    
    % m_tail pointer (below)
    \draw[->, thick] (4, -3.2) -- (4, -2.8);
    \node[anchor=north] at (4, -3.2) {m\_tail = 4};
    
    % Status
    \node[anchor=north] at (4, -3.8) {Status: 3 elements (m\_tail > m\_head)};
    \node[anchor=north] at (4, -4.2) {Note: Index 0 is now "stale" (logically removed)};
\end{tikzpicture}

Most of the time, when we advance an index like this, it is a simple increment. But, as I stated earlier, the buffer slots are used in a a circular fashion. If that increment would place that index out of bounds, it wraps around to the zeroeth slot (that’s what makes it a ring) of the queue buffer.

Show the code

%%itikz --temp-dir --tex-packages=tikz --tikz-libraries=arrows.meta --implicit-standalone
\begin{tikzpicture}[font=\small\ttfamily]
    \fill[white] (-2, 0.5) rectangle (8.5, -4.8);
    % Title
    \node[anchor=north] at (4, 0) {\textbf{SPSC Ring Buffer (7 elements)}};
    
    % m_head pointer (above)
    \node[anchor=south] at (1, -0.8) {m\_head = 1};
    \draw[->, thick] (1, -1.0) -- (1, -1.4);
    
    % Index labels
    \node[anchor=east] at (-0.2, -1.5) {Index:};
    \foreach \i in {0,...,7} {
        \node at (\i, -1.5) {\i};
    }
    
    % Buffer cells
    \node[anchor=east] at (-0.2, -2.5) {Buffer:};
    \foreach \i in {0,...,7} {
        \draw (\i-0.4, -2.2) rectangle (\i+0.4, -2.8);
    }
    % Fill cells 1-7
    \fill[lightgray!30] (0.6, -2.2) rectangle (1.4, -2.8);
    \fill[lightgray!30] (1.6, -2.2) rectangle (2.4, -2.8);
    \fill[lightgray!30] (2.6, -2.2) rectangle (3.4, -2.8);
    \fill[lightgray!30] (3.6, -2.2) rectangle (4.4, -2.8);
    \fill[lightgray!30] (4.6, -2.2) rectangle (5.4, -2.8);
    \fill[lightgray!30] (5.6, -2.2) rectangle (6.4, -2.8);
    \fill[lightgray!30] (6.6, -2.2) rectangle (7.4, -2.8);
    \node at (1, -2.5) {2};
    \node at (2, -2.5) {3};
    \node at (3, -2.5) {5};
    \node at (4, -2.5) {8};
    \node at (5, -2.5) {13};
    \node at (6, -2.5) {21};
    \node at (7, -2.5) {34};
    
    % m_tail pointer (below)
    \draw[->, thick] (0, -3.2) -- (0, -2.8);
    \node[anchor=north] at (0, -3.2) {m\_tail = 0};
\end{tikzpicture}

As we’ll see, it turns out that the indices m_head and m_tail will need to be atomic objects. We’ll understand why this is the case.

The storage for a ring buffer consists of a fixed-capacity array of elements and the indices for head and tail. We shall write spsc_queue as a templated class having the capacity as a template parameter.

template<typename T, size_t capacity>
class spsc_queue{
    private:
    // The capacity must be a power of two.
    static_assert((capacity & (capacity - 1)) == 0);    
    T m_buffer[capacity];
    size_t m_head;
    size_t m_tail;
    public:
        /* ... */
};

We would like to enforce the capacity to be a power of \(2\) for efficiency reasons. Remember, that with this design, there’s always atleast one unused element in the array, because m_head == m_tail + 1 is the queue full condition. So, the effective capacity equals capacity - 1.

The `class` interface

Here is the class interface:

template<typename T, size_t capacity>
class spsc_queue{
    private:
    // The capacity must be a power of two.
    static_assert((capacity & (capacity - 1)) == 0);    
    T m_buffer[capacity];
    size_t m_head;
    size_t m_tail;
    public:
        using value_type = T;
        spsc_queue();
        bool is_empty() const;
        bool is_full() const;
        bool push_back(value_type& item);
        bool pop_front();
};

`push_back()` and `pop_front()` take 1

Here’s a first attempt at implementing pop():

size_t next(size_t idx)
{
    if(++idx >= m_size)
        idx = 0;
    return idx;
}

bool pop_front()
{
    value_type v;
    if(!is_empty()){
        v = m_buffer[m_head];
        m_head = next(m_head);
        return true;
    }
    else{
        return false;
    }
}

Unfortunately, this section of code for advancing m_head has a couple of problems. The increment of m_head could be pre-empted in the middle. And that’s a problem because the push thread also reads the m_head index in order to figure out, whether the queue is full.

Note that, push_back() is always called by the producer thread while pop_front() is always called by the consumer thread.

That’s why, the spsc_queue’s design depends on:

Reading and writing the indices non-pre-emptively.
Having only one producer thread and one consumer thread.

if the consumer thread is pre-empted while writing m_head, the producer thread may read a half-written nonsense value.

bool push_back(value_type& v)
{
    if(!is_full()){
        m_buffer[m_tail] = v;
        m_tail = next(m_tail);
        return true;
    }
    else{
        return false;
    }
}

If the producer thread is pre-empted while writing m_tail, the consumer thread may read a half-written nonsense value.

Using atomic indices

This is my implementation for SPSC lock-free queue with atomic indices.

#include <atomic>
#include <thread>

template<typename T, size_t capacity>
class spsc_queue{
    private:
    // The capacity must be a power of two.
    static_assert((capacity & (capacity - 1)) == 0);    
    T m_buffer[capacity];
    alignas(std::hardware_destructive_interference_size) std::atomic<size_t> m_head;
    alignas(std::hardware_destructive_interference_size) std::atomic<size_t> m_tail;

    public:
        using value_type = T;
        spsc_queue()
        : m_buffer{}
        , m_head{0}
        , m_tail{0}
        {}

        [[nodiscard]] bool is_empty() const{
            return m_head.load()
                == m_tail.load();
        }

        [[nodiscard]] bool is_full() const{
            return m_tail.load() + 1 == m_head.load();
        }

        [[nodiscard]] size_t get_size(){
            return m_tail.load() - m_head.load() + 1;
        }

        [[nodiscard]] size_t get_capacity(){
            return capacity - 1;
        }

        [[nodiscard]] size_t next(size_t current_idx)
        {
            size_t next_idx = current_idx & (capacity - 1);
            return next_idx;
        }

        bool push_back(value_type& item){
            size_t tail = m_tail.load(std::memory_order_relaxed);
            size_t next_write_index = next(tail);
            if(next_write_index == m_head.load(std::memory_order_acquire))
                return false;

            m_buffer[tail] = item;
            m_tail.store(next_write_index, std::memory_order_release);
            return true;
        }

        bool pop_front(value_type& v){
            size_t head = m_head.load(std::memory_order_relaxed);
            if(head == m_tail.load(std::memory_order_acquire))
                return false;

            v = m_buffer[head];
            size_t next_read_index = next(m_head);
            m_head.store(next_read_index, std::memory_order_release);
            return true;
        }
};

Why do we use a power of \(2\) buffer size?

For a buffer of fixed capacity \(N\), with current index idx, the index to the next element can be calculated as:

next_idx = (curr_idx + 1) % N

This is because our queue is a ring buffer, so after the last slot, we will go back to the zeroeth one, then the first one and so on.

We can use the above method to get the next index for any buffer size \(N\). Why do we then only use capacity that are powers of \(2\)? The answer is easy: performance. The modulo (%) operator requires a division instruction, which is expensive. When the size \(N\) is a power of \(2\), we can just do the following:

size_t next_index = curr_index & (N - 1);

Buffer access synchronization

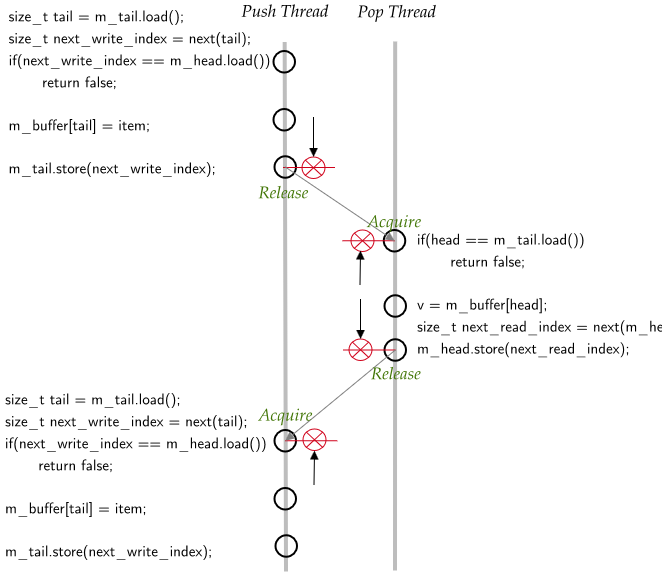
Here’s what the actual execution order looks like after we make the indices atomic.

If we look at the push thread, the incremented value of the tail, next_write_index written to m_tail index is a release operation. Over on the pop thread, when we load the m_tail index (take a snapshot of it), this is an acquire operation. The combination of release and acquire on the same atomic variable implies that m_tail store in the push thread synchronizes with m_tail load on the pop thread.

The instruction m_buffer[tail] = item cannot be moved to after the release barrier in actual CPU execution order. The instrusction v=m_buffer[head] cannot be moved to before the acquire barrier in actual CPU exection order. So, we have happens-before relationship between these two instructions.

The release of m_head in the pop thread synchronizes with the acquire of m_head in the push thread.

Designing the spsc_queue data-structure

What makes an operation atomic?

Setup - How the queue works

The class interface

push_back() and pop_front() take 1

Using atomic indices

Why do we use a power of \(2\) buffer size?

Buffer access synchronization

Designing the `spsc_queue` data-structure

The `class` interface

`push_back()` and `pop_front()` take 1